资源解耦的联邦学习:一种新型三方博弈激励机制解读
论文复盘|Data Assetization via Resources-Decoupled Federated Learning
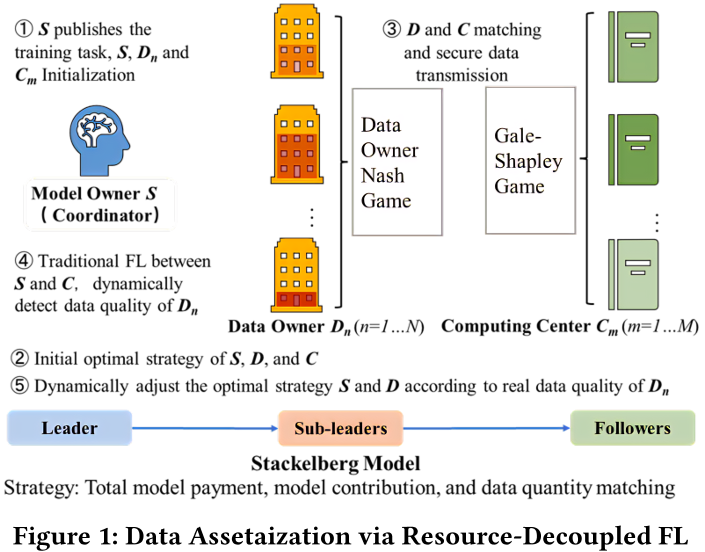
Data Assetaization via Resource-Decoupled FL
主要创新点
提出了“资源解耦联邦学习”框架
- 不同于传统联邦学习假设每个参与者既拥有数据又具备计算能力,本文考虑到了数据资源和计算资源的分离——即数据拥有者没有算力,计算中心没有数据。
- 我们构建了一个由三方组成的新型框架联邦学习:
- 模型拥有者 (Model Owner):负责协调整体FL流程,设定激励策略。
- 数据拥有者 (Data Owner):提供不同质量和数量的数据,但计算能力有限。
- 计算中心 (Computing Center):提供计算资源,与数据拥有者匹配完成训练任务。
构建三方博弈模型(Tripartite Stackelberg Model)
- 本文提出了一个三层Stackelberg 博弈模型
- 模型拥有者为领导者,决定奖励总额
- 数据拥有者为第二层领导者,决定贡献数据的数量和质量
- 计算中心为跟随者,决定是否参与和匹配数据
设计质量感知的动态资源解耦联邦学习算法(QR-RDFL)
- QR-RDFL: Quality-aware dynamic resource-decoupled FL algorithm
- 初始节点,根据数据拥有者报告的质量进行策略的生成
- 训练过程中,通过真实训练loss动态调整数据质量评估
- 使用Gale-Shapley算法对数据拥有者和计算中心进行一对一匹配
研究方法
问题陈述
全局效用优化 (Global Utility Optimization)
- 我们设计的资源解耦的联邦学习目标是通过最小化全局损失函数来优化全局模型参数$w^*$
- 全局损失函数如下公式所示,是通过所有计算中心的训练损失的加权平均计算得来的。
- 其中$p_i=\frac{x_n}{\sum_Kx_n}$,即为数据拥有者$D_n$贡献的数据占所有数据的比例
计算中心效用 (Utility of Computing Center)
\[\begin{cases} \displaystyle \arg\max_{d_m} U_m(d_m) = \lambda \cdot \frac{d_m}{\sum_{m=1}^{M} d_m} \cdot \sum_{n=1}^{N} \rho x_n - \varepsilon \sigma_m d_m, \\\\ \text{s.t.} \quad \rho \geq 0 \end{cases}\]s.t. 表示subject to,意为“满足如下约束条件”
| 符号 | 描述 | 作用 |
|---|---|---|
| $\lambda$ | Market regulating factor | 用于调节数据拥有者和计算中心的成本-收益关系 |
| $d_m$ | 计算中心$C_m$承担的数据量 | \ |
| $\rho$ | 单位数据量支付给计算中心的报酬 | \ |
| $\varepsilon$ | 使用单位数据量进行训练时,计算中心需要支付的成本 | \ |
| $\sigma_m$ | 计算中心的算力 | \ |
数据拥有者效用 (Utility of Data Owner)
\[\begin{cases} \displaystyle \arg\max_{q_n} \quad U_n(q_n, q_{-n}) = \frac{q_n}{\sum_{n=1}^{N} q_n} \cdot \eta - \lambda \rho x_n, \\\\[10pt] \text{s.t.} \quad \begin{cases} q_n = f_n x_n, \\\\ 0 < x_n < |X_n|, \\\\ f_n \geq \xi. \end{cases} \end{cases}\]| 符号 | 描述 |
|---|---|
| $q_n$ | 每个数据拥有者对全局模型的贡献 |
| $f_n$ | 贡献的数据质量 |
| $x_n$ | 贡献的数据量(quantity) |
| $q_{-n}$ | $q_{-n}={q_1, q_2, …, q_{n-1}, q_{n+1}, …, q_N}$,所有贡献除了数据拥有者$D_n$的贡献的序列 |
| $\eta$ | 模型拥有者的总支付 |
模型拥有者效用 (Utility of Model Owner)
- 全局模型越好越有价值,但得控制激励成本 $\eta$。
| 符号 | 描述 |
|---|---|
| $\alpha$ | 全局模型质量对收益的敏感度(正数) |
| $g(x)$ | 模型质量的效用函数,通常设为$ln(1+x)$ |
三方 Stackelberg 模型(Tripartite Stackelberg Model)
- 为三方构建了Stackelberg博弈模型,并定义了Stackelberg-Nash均衡来获取全局最优值
- 策略配置为$\langle \eta^, Q^, G^* \rangle$,策略实施步骤如下
- 第一步:模型拥有者首先确定全局最优奖励$\eta^*$
- 第二步:数据拥有者们之间进行Nash均衡博弈,决定提供的数据质量和数据量,也就是每个数据拥有者对于全局模型的贡献$q^*_n$
- 第三步:每个算力中心根据最优承担的数据量$d^_m$,选择一个特定的数据拥有者,并建立最优匹配关系$G_m^$
- 我们将资源解耦型的联邦学习定义为三方Stackelberg模型,其中:
- 模型拥有者作为领导者
- 数据拥有者作为次级领导者
- 计算中心作为跟随者
定义 1:Tripartite Stackelberg Model
\[\begin{cases} \textit{Leader } S:\quad \eta^* = \arg\max_{\eta} U_s, \\\\[8pt] \textit{Sub-Leaders } D_n:\quad q_n^* = \arg\max_{q_n} U_n, \quad n = 1, \dots, N, \\\\[8pt] \textit{Followers } C_m:\quad G_m^* = \arg\max_{G_m} U_m, \quad m = 1, \dots, M. \end{cases}\]- 定义1说明了,每个参与方都是力求自己的效用最大
定义 2:Stackelberg-Nash Equilibrium 的条件表达式
\[\begin{cases} U_s(\eta^*, Q^*, G^*) \geq U_s(\eta, Q^*, G^*), \\\\ U_n(\eta^*, q_n^*, q_{-n}^*, G^*) \geq U_n(\eta^*, q_n, q_{-n}^*, G^*), \quad n = 1, \dots, N, \\\\ U_m(\eta^*, Q^*, G_m^*) \geq U_m(\eta^*, Q^*, G_m), \quad m = 1, \dots, M. \end{cases}\]- 上式说明了,三方博弈模型中任意一方不能通过自己的策略来获得更好的收益
三方层级博弈模型解析 (Analysis of Tripartite Stackelberg Model)
- 根据逆向归纳法,我们:
- 首先,求解出每个计算中心的最优$d_m^*$
- 然后,计算出每个数据拥有者的最优$q_n^*$
- 最后,是模型拥有者的最优$\eta^*$
引理1:对于每一个计算中心,给定从数据拥有者获得的数据量,都有一个特定的最优$d_m^*$使得计算中心的效用能够最大
- 对于计算中心来说,决策空间就是每个计算中心所能选择的数据量
- 数据量的范围是一个有界的,连续的,封闭的
- 公式7、8是效用函数对数据量$d_m$的一阶导数和二阶导数
- 公式8说明效用对于$d_m$的二阶导是小于0的
- 那么效用函数就是一个凹函数,存在极大值点
引理2:对于一个数据拥有者$q_n$,给定$\eta$和$q_{-n}$,存在一个最优策略$q_n^*$来最大化数据拥有者的$U_n$
-
对于每个数据拥有者的决策空间,是一个连续的,封闭的,有界的区间$[0, X_n ]$
- 通过求解可以得到
引理3:对于模型拥有者,给定参数$\alpha$和客观的有数据拥有者$f_n$提供的数据质量,存在一个最优的$\eta^*$使得模型拥有者的效用$U_s$最优
- $\eta$的范围是$[0, +\infty]$,但是由于边际递减效应和从实际角度来讲模型拥有者并不会给出无限多的报酬,所以$\eta$的范围也应该是有界的,封闭的和连续的
- 公式13和14分别为模型拥有者的效用函数对于$\eta$的一阶导和二阶导
- 最后,解得$\eta^*$如公式15所示:
QD-RDFL
- 在本节中,我们设计了QD-RDFL算法来识别最优strategy profile,其中设计了一种动态优化机制,通过评估数据所有者的模型贡献来提高最优策略。
- 为了检验数据的实际贡献,最精确的方法是使用本地模型在验证集上测试精确度,但是这种方法会带来更大的成本
- 所以我们选择使用训练损失来作为评估$f_n$的指标
- QD-RDFL算法总共有5步:
- 初始化:模型拥有者S分发任务,初始化$S,\ D_n,\ C_m$
- 初始化最优策略:$S,\ D,\ C$首先计算出一个初始策略
- 使用Gale-Shapley算法匹配数据和算力资源:数据和算力中心根据初始化的最优策略进行匹配
- 联邦学习和数据质量评估:模型拥有者和计算中心进行传统联邦学习
- 动态调整最优策略:$S,\ D,\ C$根据实际的训练结果调整最优策略
\begin{algorithm}
\caption{QD-RDFL: Quality-aware Dynamic Resources-Decoupled Federated Learning}
\begin{algorithmic}[1]
\REQUIRE Data owners $D_n\ (n = 1, \dots, N)$, computing centers $C_m\ (m = 1, \dots, M)$, parameters $\rho, \varepsilon, \alpha, \lambda$, adjustment round $L$
\ENSURE Optimal strategy profile $\langle \eta^*, Q^*, G^* \rangle$
\STATE Initialize $S, D, C$, and let each data owner report initial $f_n$
\STATE Compute $\eta^*$ according to Equation (15)
\STATE Compute $x_n^*$ for each $D_n$ according to Equation (12)
\STATE Compute $d_m^*$ for each $C_m$ according to Equation (9)
\STATE Compute $G^* = \textsc{Gale-Shapley}(D_n, C_m)$
\FOR{each data owner $D_n,\ n \in [1, N]$}
\STATE Randomly pick $x_n^*$ and transfer data based on $G^*$
\ENDFOR
\FOR{each round $t = 1, 2, \dots, T$}
\FOR{each computing center $C_m,\ m \in [1, M]$}
\STATE $(w_m^{t+1}, f_m^{t+1}) \leftarrow \textsc{ClientUpdate}(C_m, w^t)$
\ENDFOR
\IF{$t = L$}
\STATE Normalize each $f_n$, recalculate $\eta^*$ and $x_n^*$
\IF{$x_t^* > x_t$}
\STATE Pay additional training fees
\ENDIF
\ENDIF
\STATE $w^{t+1} \leftarrow \frac{1}{M} \sum_{m=1}^{M} w_m^{t+1}$ \COMMENT{Global model aggregation}
\ENDFOR
\end{algorithmic}
\end{algorithm}
\begin{algorithm}
\caption{ClientUpdate}
\begin{algorithmic}[1]
\REQUIRE Computing center $C_m$, global model parameter $w$, start time $t_s$, end time $t_e$
\ENSURE Updated local model $w_m$, data quality contribution $f_m$
\STATE $w_m \leftarrow w$
\FOR{each local epoch $i$ from $1$ to $E$}
\STATE $w_m \leftarrow w_m - \beta \nabla \mathcal{L}(w_m)$
\STATE Record $loss(t_s)$ and $loss(t_e)$
\ENDFOR
\STATE $f_m \leftarrow loss(t_s) - loss(t_e)$
\RETURN $w_m$, $f_m$
\end{algorithmic}
\end{algorithm}
附 (知识点)
Stackelberg 博弈模型
- 这种模型的决策是有顺序的
- 是一种非对称博弈模型,场景中有领导者 (leader) 和跟随者 (follower)
- 领导者先行动,跟随者看到领导者的策略后再选择自己的最优策略
- 例如:
- 企业定价 vs 消费者反应
- 政策制定 vs 市场反应
Nash 均衡 (Nash Equilibrium)
- 一种策略组合状态,在这个状态下,每个人都无法通过改变自己的状态来增加收益
- 策略是平衡的,每个人都不想变了
- 所有参与者都同时做决策,每个人都试图最大化自己的收益
- 例如:
- 石头剪刀布游戏
Stackeelberg-Nash 均衡
- 在一个复杂的系统中,我们会遇到:
- 一部分人先进行决策 —— Stackelberg
- 模型拥有者先进行定价
- 另一部分人在已知前者的策略下,与自己的同种类的参与者进行竞争 —— Nash
- 多个数据拥有者之间进行竞争
- 一部分人先进行决策 —— Stackelberg
- 因此,出现了一个结合的状态 Stackelberg-Nash均衡(NSE)
Gale-Shapley 算法
- 又叫延迟接受算法 / 稳定婚姻匹配算法,用于解决双边匹配算法
- 目标:在两个群体之间,找到一个稳定匹配(每个稳定匹配中包含多组两两匹配)
- 稳定:已配对的两个个体不会打破形成的匹配,去选择另外另外的个体
- 算法的基本流程,以“男追女”作为说明:
- 所有人都有一个偏好列表,例如$M_1$喜欢$W_1 > W_2 > W_3$
- 在每一轮中:
- 每位男士会向他最喜欢的、还没拒绝他的女士发出邀请
- 每位女士会收到多个提议,并“暂时接受”她最喜欢的那个人,拒绝其余的(注意:女士也有一个偏好列表)
- 被拒绝的男士下一轮喜欢的对象
- 持续进行,直至:
- 所有人都匹配成功
- 没有人再提出新的请求
- 最终形成的匹配是稳定且最优的(对主动方而言)