前言

• 被这个二分查找折磨得实在是不成样子了，感觉题目很难想出来，题目即使ac了也感觉莫名奇妙的

思想

整数二分

• 整数二分的本质：给定一个性质，将一个区间划分为满足该性质和不满足该性质的两个区间，通过二分可以查找到区间的边界。如图所示，下图的红绿边界的端点都可以被找到，对应不同的模版

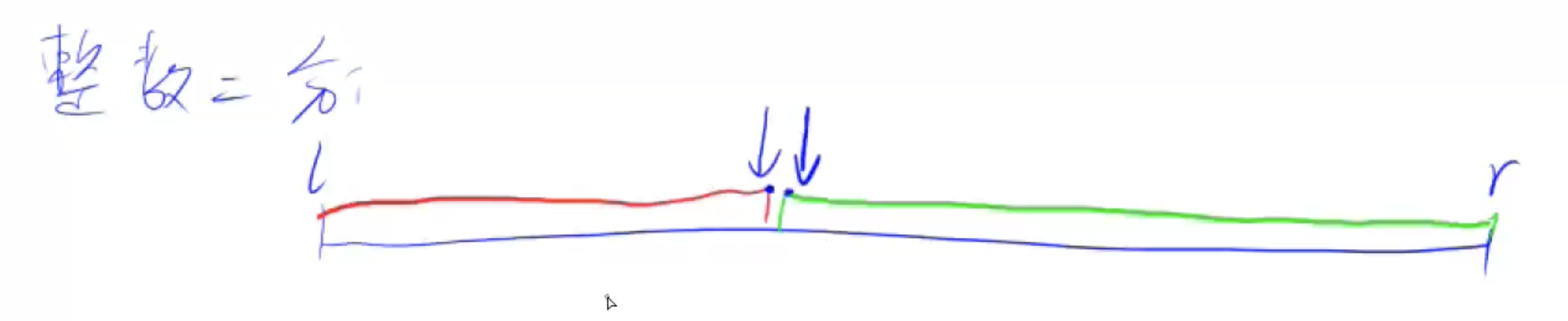
寻找红色边界端点

• 初始化l = 0, r = vec.size(), mid = (l + r + 1) / 2

• 判断mid指向的元素是否符合红色区域性质
  • 如果符合，则说明红色区间端点位于[mid, r]，更新l = mid
  • 如果不符合，则说明红色区间端点位于[l, mid - 1]，更新r = mid - 1

为什么要+ 1呢？

• 当l = r - 1时，mid = (l + r) / 2的计算结果为(l+r)/2 = (r-1+r)/2 = r-1 = l
• 此时，若check(mid)返回true，则将进入死循环
• 当+ 1之后，mid = (l + r + 1) / 2 = r，更新后l = r，可以中止循环

寻找绿色边界端点

• 初始化mid = (l + r) / 2 \(mid =\frac{l+r}{2}\)
• 判断mid指向的元素是否满足绿色区域性质
  • 如果符合，则说明绿色边界端点位于[l, mid]之间，更新r = mid
  • 如果不符合，则说明绿色边界端点位于[mid + 1, r]， 更新r = mid + 1

解题心路历程

• 写一个check函数
• 根据check函数中定义的要获取哪个区间的端点，来确定mid是否需要+ 1
  • 如果寻找的是红色区间端点，那么就需要+ 1
  • 如果寻找的是绿色区间端点，那么就不需要+ 1

模版

寻找红色边界端点

int main(){
    int l = 0, r = vec.size() - 1;
    while(l < r){
        int mid = (l + r + 1) / 2;
        if(nums[mid] <= target)
            l = mid;
        else
            r = mid - 1;
    }

    cout << l << endl;
}

为什么l一定能等于r

• 假设l = r - 1，那么mid = (l + r + 1) / 2 = r
• 两种更新方式：
  • l = mid: 那么l = r
  • r = mid - 1: 那么r = r - 1 = l

为什么l == r（循环中止的时候），l指向的元素一定是端点

• 证明$\text{nums}[l]\leq \text{target}, \text{nums}[r+1] > target$
• 假设在第k次循环中，$\text{nums}[l]\leq \text{target}, \text{nums}[r+1] > target$成立
  • 如果$\text{nums}[mid] \leq \text{target}$，那么$l = mid$
    • 对于$\text{nums}[l]\leq \text{target}$：$\text{nums}[l] = \text{nums}[mid]\leq \text{target}$，依旧成立
    • 对于$\text{nums}[r+1] > target$：$r$没变，依旧成立
  • 如果$\text{nums}[mid] > \text{target}$，那么$r = mid - 1$
    • 对于$\text{nums}[l]\leq \text{target}$：$l$没变，依旧成立
    • 对于$\text{nums}[r+1] > \text{target}$：$\text{nums}[r+1] = \text{nums}[mid]>\text{target}$，依旧成立
• 在循环中止时，$l = r$，此时$\text{nums}[l]\leq \text{target},\text{nums}[r+1]=\text{nums}[l+1]>\text{target}$，所以$l$就是所求区间的端点

寻找绿色边界端点

int main(){
    int l = 0, r = vec.size() - 1;
    while(l < r){
        int mid = (l + r) / 2;
        if(nums[mid] >= target)
            r = mid;
        else
            l = mid + 1;
    }

    cout << l << endl;
}

为什么l一定能等于r

• 假设l = r - 1，此时mid = (l + l + 1) / 2 = l
• 两种更新方式：
  • r = mid: 那么r = mid = l
  • l = mid + 1: 那么l = l + 1 = r

为什么l == r（循环中止的时候），l指向的元素一定是端点

• 证明nums[l - 1] < target（l > 0）, nums[r] >= target
• 初始
  • 两个条件一定符合
• 循环中
  • 假设对于第k次
    • nums[l - 1] < target成立
      • 在第k + 1次中，如果更新r，那么nums[l - 1] < target依旧成立;如果更新l，那么说明nums[mid] < target，此时l - 1 = mid，所以nums[l - 1] = nums[mid] < target
      • 得证
    • nums[r] >= target成立
      • 如果更新l，那么依旧成立；如果更新r， r = mid， nums[r] = nums[mid] >= target
      • 得证
• 循环结束时，由于前面的证明，我们知道nums[l - 1] < target, nums[r] >= target，由于l = r，那么nums[l - 1] < target, nums[l] >= target
• 综上，我们可以说l指向的元素就是我们查找的红色区间的端点

刷题

LeetCode

搜索二维矩阵

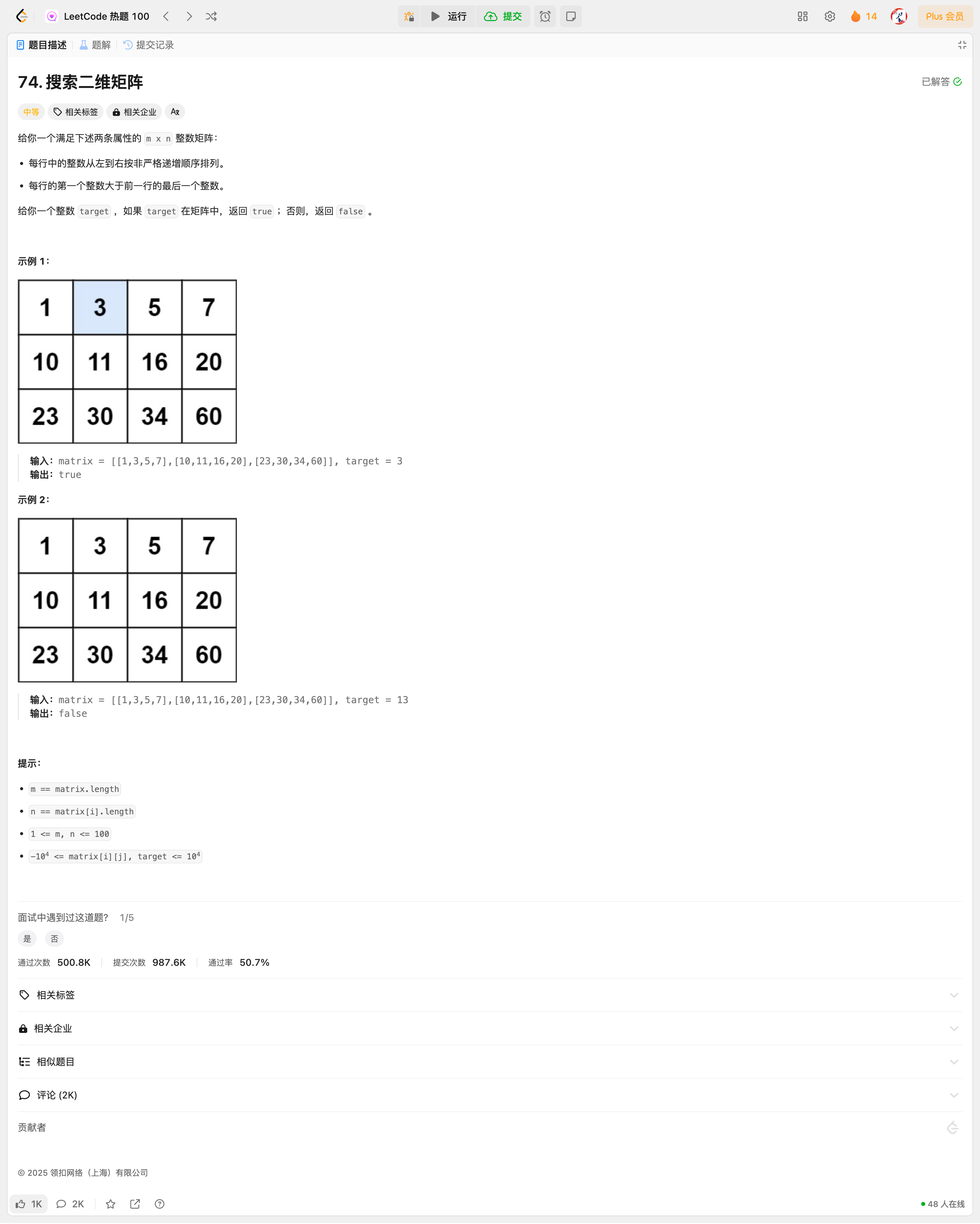
知识点

解题思路

• 首先确定要划分的左右区间，左边区间为<= target，右边区间为> target
• 我们要寻找的就是左侧区间端点，只有左侧区间端点才有可能等于target，如果端点不等于，那么该矩阵中就没有target
• 根据分析，此时mid = (l + r + 1) / 2，经过一系列迭代后，l == r退出循环
• 返回l，即为端点值

实现代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {

        int l = 0, r = matrix.size() - 1;

        while(l < r){
            int mid = (l + r + 1) / 2;

            if(matrix[mid][0] <= target){
                l = mid;
            }else{
                r = mid - 1;
            }
        }

        if(matrix[l][0] == target)
            return true;


        int index = l;

        l = 0, r = matrix[index].size() - 1;
        while(l < r){
            int mid = (l + r + 1) / 2;

            if(matrix[index][mid] <= target){
                l = mid;
            }else{
                r = mid - 1;
            }
        }

        if(matrix[index][l] == target)
            return true;
        else
            return false;
    }
};

AcWing

730. 机器人跳跃问题

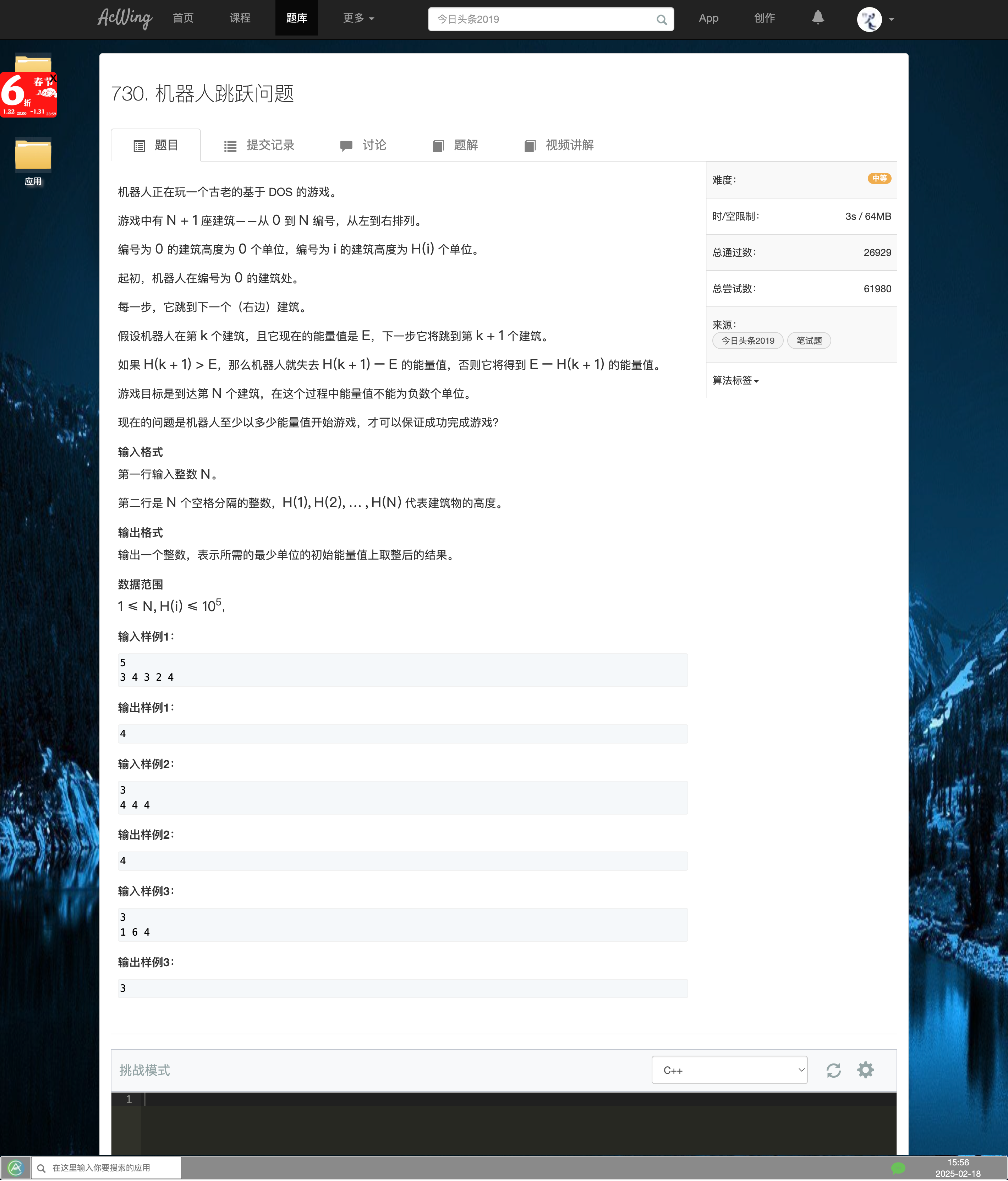
知识点

• long long类型在printf函数中的替换符为%lld

解题思路

• 根据题意可知，我们要寻找的是最小的可以让机器人跳跃到最后一个塔顶的e
• 分析后可知，e具有单调性，即越大越好，所以我们可以采用二分进行查找
• 划分范围，此题我们可以用寻找右侧部分端点思维进行思考，即寻找最小的符合条件的e，右侧区间均为可以使机器人跳跃到最后塔顶的e值，左侧区间内的值均无法保证机器人可以跳跃到最后塔顶
• 设计check函数：
  • 第一次设计：初次设计时，未考虑爆int的情况，导致计算到后续塔位置时，即使符合条件的值也会被筛选掉
  • 第二次设计：采用long long类型进行计算，发现治标不治本，考虑剪枝
  • 第三次设计：当e值大于h数组中最大的元素时（遍历时获得），此时一定可以跳跃到最后塔顶，直接返回true

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;
typedef long long ll;
int h[N];
int n, MAXE;

bool check(int e){
    // cout << "进入check函数" << endl;
    // cout << "此时e为：" << e << endl;
    // 检查能否通过

    // ll sum = e;

    for(int i = 0; i < n; i ++){
        if(h[i + 1] > e)
            e -= (h[i + 1] - e);
        else
            e += (e - h[i + 1]);

        // printf("h[%d]时候的sum是多少:%lld \n", i + 1, sum);
        if(e < 0)
            return false;
        else if(e > MAXE)
            return true;
    }

    return true;
}


int main(){
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n;
    int l = 0, r = 0;
    h[0] = 0;

    for(int i = 1; i <= n; i ++){
        cin >> h[i];
        r = max(r, h[i]);

    }
    MAXE = r;

    while(l < r){
        int mid = (l + r) / 2;
        if(check(mid))
            r = mid;
        else
            l = mid + 1;
    }

    cout << l << endl;


    return 0;
}

参考资料链接

• AcWing: 二分查找-数的范围课程
• AcWing: 二分查找算法模板By Yxc
• CSDN博客：不需要考虑mid + 1, mid - 1的二分查找模版
• B站视频：二分查找为什么总是写错？
• AcWing-题解-数的范围（详细分析二分过程）

草纸

• r = l + 1;
• mid = (l + r) / 2 = (2l + 1) / 2 = l