区间问题

区间选点

知识点

解题思路

贪心算法：
- 可以先试一试一些做法，万一就试出来了呢？
对于本道题：
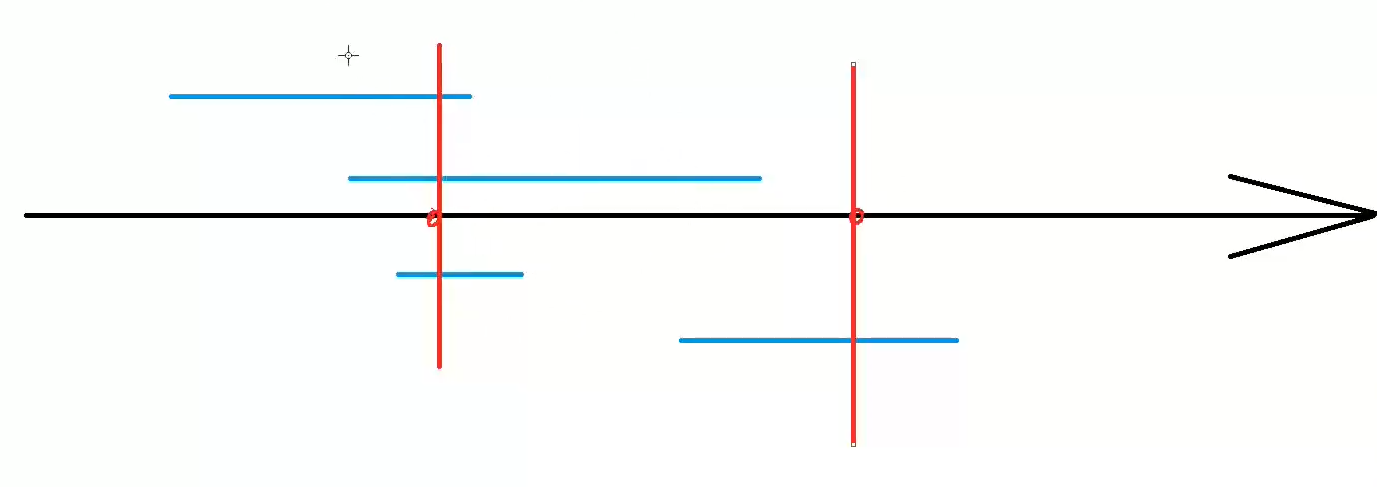
- 先将每个区间的右端点按从小到大进行排序
- 从前往后依次枚举每个区间
  - 如果当前区间中已经包含点，则直接pass
  - 否则选择当前区间的右端点
数学证明：
- 如果想要证明$A=B$，可以分别证明$A\geq B$和$A \leq B$
- 设$\text{cnt}$是所有可能方案的选点数，$\text{Ans}$是所有可能方案中的最小值
- 所以我们有$\text{Ans} \leq \text{cnt}$（这个不用证明）
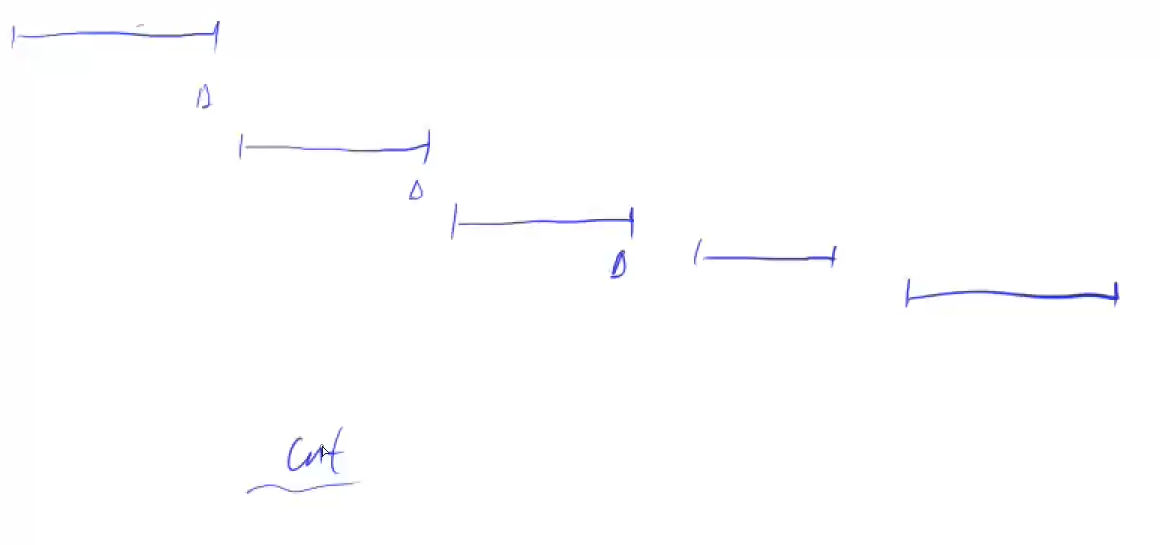
- （这个根据新加进来的规则进行证明）对于第二种情况“否则选择当前区间的右端点”，如下图所示，对于任意$\text{cnt}$，我们可以找到$\text{cnt}$个区间（从左至右排列，两两彼此之间互不相交）
- 那么最优解的下界就是这些区间上必须都有一个点，才可以覆盖这些区间
- 所以，$\text{Ans} \geq \text{cnt}$
- 综上，$\text{Ans} = \text{cnt}$，即通过这种策略选出来的点就是最优解

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;
int n;
struct Range{
    int l, r;
    bool operator< (const Range &W) const{
        return r < W.r;
    }
}range[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        scanf("%d%d", &range[i].l, &range[i].r);
    }

    sort(range, range + n);

    int res = 0, ed = -2e9;
    for(int i =0; i < n; i ++){
        if(range[i].l > ed){
            res ++;
            ed = range[i].r;
        }
    }

    cout << res << endl;
    return 0;
}

最大不相交区间数量

知识点

解题思路

我们的贪心规则是：
- 如果当前区间被已选中的区间部分覆盖了，那么就跳过该区间
- 如果没有被覆盖，那么就选择该区间，并将该区间的右侧端点作为边界值进行判断
我们假设按照以上规则选出的区间个数为$Cnt$个，最优解（最大值）的区间个数为$Ans$个
- 那么根据定义，我们可以轻松得到$Ans \geq Cnt$
- 根据我们的贪心规则，已经将所有的不相交的区间挑选出来了，所以最优解的上界就是$Cnt$，所以$Ans \leq Cnt$
- 综上，我们可以得到$Ans = Cnt$，即根据我们的贪心规则，挑选出来的就是最优解

实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 100;

struct Range{
    int l, r;
    bool operator< (const Range &W) const{
        return r < W.r;
    }
}range[N];

int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++)
        scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n);

    int ans = 0, ed = -2e9;
    for(int i = 0; i < n; i ++){
        if(range[i].l > ed){
            ans ++;
            ed = range[i].r;
        }
    }

    cout << ans << endl;
    return 0;
}

区间分组

知识点

解题思路

首先将所有区间按照左端点从小到大进行排序
我们的贪心规则为：
- 如果当前区间有一部分（左端点小于组的最右侧端点）与最新建立的组有部分重合，那么就建立一个新的组存放这个区间
- 如果当前区间没有重合，那么就将这个区间放入组中
数学证明：
- 假设我们根据这个规则选出来的组有$Cnt$个，最优解（最小值）的区间有$Ans$个
- 那么根据定义，可以得到$Ans \leq Cnt$
- 根据我们指定的规则，我们至少会有$Cnt$个组，这就得到了$Ans$的下界，即$Ans \geq Cnt$
  - 假设有$Cnt - 1$个组，那么必定会有一个组具有重叠的部分，这与题设不符合，所以不成立
  - 假设有$Cnt + 1$个组，那么就要从一个组选出一个区间，但是这个区间是可以加入原来的组，这与最小值的定义就不相符合了
- 综上，$Ans = Cnt$

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;
struct Range{
    int l, r;
    bool operator< (const Range &W) const{
        return l < W.l;
    }
}range[N];

int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++)
        scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n);

    priority_queue<int, vector<int>, greater<int>> heap;

    for(int i = 0; i < n; i ++){
        // 由于排序的完成，所有区间都是按照左端点从小到大已经排好序了
        // 如果当前区间的左端点小于最新组的右端点
        if(heap.empty() || heap.top() >= range[i].l)
            heap.push(range[i].r);
        else{
            heap.pop();
            heap.push(range[i].r);
        }
    }

    cout << heap.size() << endl;

    return 0;
}

区间覆盖

知识点

解题思路

贪心规则：
- 将所有区间按左端点从小到大进行排序
- 从前往后依次枚举每个区间，在所有能覆盖start的区间中，选择一个右端点最大的区间，然后将start更新成右端点的最大值
数学证明：
- 设根据规则选出来的区间数为$Cnt$个，最优解（最小值）为$Ans$个
- 根据题意，必有$Ans \leq Cnt$
- 根据我们的规则$Ans \geq Cnt$

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;
struct Range{
    int l, r;
    bool operator< (const Range &W) const{
        return l < W.l;
    }

}range[N];

int main(){
    int st, ed, n;
    cin >> st >> ed;
    cin >> n;
    for(int i = 0; i < n; i ++)
        scanf("%d%d", &range[i].l, &range[i].r);


    sort(range, range + n);

    int res = 0;
    bool flag = false;

    for(int i = 0; i < n; i ++){
        int j = i, r = -2e9;
        while(j < n && range[j].l <= st){
            r = max(r, range[j].r);
            j ++;
        }


        if(r < st){
            res = -1;
            break;
        }

        res ++;

        if(r >= ed){
            flag = true;
            break;
        }

        st = r;
        i = j - 1;
    }

    if(!flag)
        res = -1;

    cout << res << endl;
    return 0;
}

Huffman 树

合并果子

知识点

解题思路

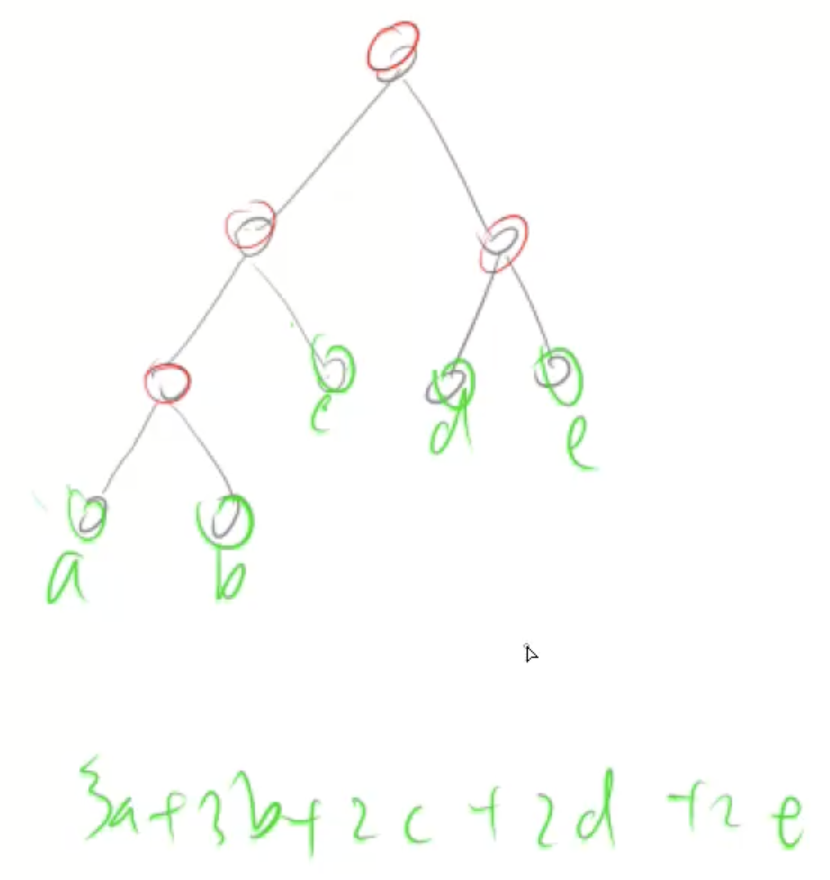
可以看到上图中的数中的叶子结点都是给定的果子，中间节点都是合并之后的果子
最后消耗的总体力值为 $3a+3b+2c+2d+2e$
以上问题可以转化为哈夫曼问题
- 最小值一定在最深的位置
- 具有最优子结构

实现代码

#include <bits/stdc++.h>
using namespace std;



int main(){
    int n;
    cin >> n;
    priority_queue<int, vector<int>, greater<int>> heap;

    for(int i = 0;i < n; i ++){
        int x;
        scanf("%d", &x);
        heap.push(x);
    }

    int res = 0;
    while(heap.size() > 1){
        int a = heap.top();
        heap.pop();
        int b = heap.top();
        heap.pop();
        res += a + b;
        heap.push(a + b);
    }

    cout << res << endl;
    return 0;


}

排序不等式

排队打水

知识点

一定要注意：如果使用while(n --)进行循环，那么之后n就已经为0了，如果后续还要使用到n，那么一定不可以使用while(n --)

解题思路

按照从小到大进行排序，总时间最小
数学证明：
- 假设我们所有元素不是从小到大进行排序的，然后存在一个最优序列
- 那么就必然存在两个等待时间前一个大于后一个，即：$t_i > t_{i+1}$
- 则对于该区间的等待时间为$T_{wait} = (n-1)\times t_1 +\dots+(n-i)\times t_i+(n-i-1)\times t_{i+1} + \dots+ t_{n-1}$
- 如果我们交换$t_i,t_{i+1}$，那么等待时间将变为$T'_{wait} = (n-1)\times t_1 +\dots+(n-i)\times t_{i+1}+(n-i-1)\times t_i + \dots+ t_{n-1}$
- 则可以发现，等待时间变小了$T_{wait} - T'_{wait}=t_i-t_{i+1} > 0$
- 与假设矛盾
- 所以所有元素必须从小到大进行排列，才能得到最优子序列

实现代码

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    cin >> n;
    priority_queue<int ,vector<int>, greater<int>> q;

    for(int i = 0; i < n; i ++){
        int x;
         scanf("%d", &x);
         q.push(x);
    }

    long long res = 0;



    for(int i = 0; i < n - 1; i ++){
        int t = q.top();
        q.pop();
        res += t * (n - 1 - i);
    }

    cout << res << endl;
}

绝对值不等式

货仓选址

知识点

绝对值不等式：
- 有一个区间$[a,b]$，当$x$位于$[a,b]$中时

解题思路

将所有位置进行排序
排序后第一个位置和最后一个位置两两成组，在组成的区间内选点
这样的就满足绝对值不等式

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;

int a[N];
int n;

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++)
        scanf("%d", &a[i]);

    sort(a, a + n);

    int res = 0;
    for(int i = 0; i < n; i ++)
        res += abs(a[i] - a[n / 2]);


    cout << res << endl;

    return 0;
}

推公式

耍杂技的牛

知识点

解题思路

每头牛的危险值计算公式为$\text{Risk}=\sum^{\text{前面的牛}}w - s$
要是每头牛的危险值越小，可以考虑：
- 体重越大的牛放在最底部
- 强壮系数越大的牛放在最底部
可以考虑将$w + s$越大的牛放在越底部
数学证明：每头牛的危险系数如下表所示

cow	before exchange	after exchange
i	$\sum^{i-1}_{j=1}w_j-s_i$	$\sum^{i-1} {j=1}w_j+w {i+1}-s_i$
i+1	$\sum^{i}{j=1}w_j-s{i+1}$	$\sum^{i-1}{j=1}w_j-s{i+1}$

对每个方格减去$\sum^{i-1}_{j=1}w_j$

cow	before exchange	after exchange
i	$-s_i$	$w_{i+1}-s_i$
i+1	$w_i-s_{i+1}$	$-s_{i+1}$

接下来我们要比较交换前和交换后的的最大值，即比较max($-s_i$, $w_i-s_{i+1}$)和max($w_{i+1}-s_i$, $-s_{i+1}$)
- 当$-s_i>w_i-s_{i+1}$时
  - max($-s_i$, $w_i-s_{i+1}$) = $-s_i$
  - 若右侧的值为$w_{i+1}-s_i$,则右侧一定大于

实现代码

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;

const int N = 50000;
int n;
PII cow[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        int w, s;
        cin >> w >> s;
        cow[i] = {w + s, w};
    }

    sort(cow, cow + n);

    int res = -2e9, sum = 0;

    for(int i = 0; i < n; i ++){
        int s = cow[i].first - cow[i].second, w = cow[i].second;
        res = max(res, sum - s);
        sum += w;
    }

    cout << res << endl;

    return 0;
}

区间问题

区间选点

知识点

解题思路

实现代码

最大不相交区间数量

知识点

解题思路

实现代码

区间分组

知识点

解题思路

实现代码

区间覆盖

知识点

解题思路

实现代码

Huffman 树

合并果子

知识点

解题思路

实现代码

排序不等式

排队打水

知识点

解题思路

实现代码

绝对值不等式

货仓选址

知识点

解题思路

实现代码

推公式

耍杂技的牛

知识点

解题思路

实现代码

Enjoy Reading This Article?