快速排序

日期：2024.11.07 我们来复习一下第一节课以及一些基础的编程知识一共分为三个步骤

找分界点（中枢值），可以取q[l], q[(l + r) / 2], q[r]
将整个区间划分为两端，使得左边都小于等于x，右边所有数都大于等于x。中间分界点的数字不一定等于x，因为分段结束的条件与x的大小无关，而是看两个指针的相对位置
递归排序左边，递归排序右边

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n;

int q[N];

void quick_sort(int q[], int l, int r){
    if(l >= r)
        return ;

    int i = l - 1, j = r + 1, x = q[(l + r) / 2];

    while(i < j){
        do i ++; while(q[i] < x);
        do j --; while(q[j] > x);
        if(i < j)
            swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}


int main(void){

    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n;

    for(int i = 0; i < n; i ++){
        cin >> q[i];
    }

    quick_sort(q, 0, n-1);

    for(int i = 0; i < n; i ++){
        cout << q[i] << " ";
    }

    return 0;
}

第k个数

找到第k个数

一些基本的量

$S_l$表示一次分段后左边段中元素的个数
$S_r$表示一次分段后右边段中元素的个数

基本原理

当$k \leq S_l$时，只需要递归左边段
当$k > S_l$时，只需要递归右边段，寻找第$k - S_l$个数

小的注意事项

在C++中，当局部变量和全局变量重名时，会优先使用局部变量

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;// 定义N为一个常量，错误点

int n, k;
int q[N];

int quick_sort(int l, int r, int k){
    if(l == r) return q[l];

    int x = q[l], i = l - 1, j = r + 1;

    while(i < j){
        do i++; while(q[i] < x);//错误点，一定是q[l]!!!
        do j--; while(q[j] > x);
        if(i < j)   swap(q[i], q[j]);
    }

    int sl = j - l + 1;
    if (k <= sl)    return quick_sort(l, j, k);
    //这里的边界要搞清楚！！左边是什么，右边是什么

    return quick_sort(j + 1, r, k - sl);

}

int main(){

    cin >> n >> k;
    for (int i = 0; i < n; ++i){
        scanf("%d", &q[i]);
    }

    cout << quick_sort(0, n - 1, k) << endl;
    return 0;
}

归并排序

思想

确定分界点 mid = (l + r) / 2
递归排序left, right
归并，合二为一

如何合二为一

将两个有序序列合二为一
双指针算法

两个有序序列，初始化两个指针指向序列的第一个元素，即min最小值
比较两个指针指向的数字哪个更小，不妨设第一个有序序列的元素更小，就将其放入答案数组中（如果是两个数字相同的话，一般是将第一个序列的数字放入答案数组）
之后第一个序列中的指针向后移动一位，继续前两步的操作，直至遍历完整个数组，之后将另外数组中所有元素

时间复杂度

$O(nlogn)$

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;

int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r){
	if(l >= r)  return;
	int k = (l + r) / 2;

	merge_sort(q, l, mid);
	merge_sort(q, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while(i <= mid && j <= r){
		if(q[i] >= q[j])
			tmp[k++] = q[i++];
		else
			tmp[k++] = q[j++];

	}
	while(i <= mid)
		tmp[k++] = q[i++];
	while(j <= r)
		tmp[k++] = q[j++];

	for(i = l, j = 0;i <= r; i++, j++){
		q[l] = tmp[j];
	}

}



int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; i++){
		scanf("%d", &q[i]);
	}

	merge_sort(q, 0, n-1);

	for(int i = 0; i < n; i++){
		printf("%d",q[i]);
	}
	return 0;
}

逆序对

一个有序对ab 其中a 严格大于 b，就称为逆序对

主要思路

分治
逆序对的类别
- 两个数同时出现在左半边
- 两个数同时出现在右半边
- 一个数在左半边，一个数在右半边
假设归并排序函数已经可以将序列排好序，并返回序列内部逆序对的个数
- 所有逆序对的个数应该是三种逆序对个数的之和
- 都在左半边：直接返回merge_sort(L, mid)
- 都在右半边：直接返回merge_sort(mid + 1, R)
- 一半在左，一半在右的情况：
  - 我们从第二序列（右半边序列）看起，假设第二序列一共有m个点，从第1个点开始，在第一序列（左半边序列）中查找比第1个点大的数，那么这个数和第1个点就能构成逆序对，在第一序列中这些数字的个数记为$S_1$，以此类推，直到找到$S_m$，这种逆序对的个数即为$\sum^{n}_{i=1}S_i$
  - 那么如何快速算出$\sum^{n}_{i=1}S_i$？
    - 通过归并排序，第一个序列中第一个大于第二序列中某一数的数后面的数字，一定都大于第二序列，直接mid - i + 1

代码实现

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e5 + 100;
int n;
int q[N], tmp[N];


LL merge_sort(int l, int r){
    if (l >= r)
        return 0;

    int mid = (l + r) / 2;

    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r){
        if(q[i] <= q[j])
            tmp[k++] = q[i++];
        else{
            tmp[k++] = q[j++];
            res += mid - i + 1;
        }
    }
    while(i <= mid){
        tmp[k++] = q[i++];
    }
    while(j <= r){
        tmp[k++] = q[j++];
    }

    for(i = l, j = 0; i <= r; i++ ,j++){
        q[i] = tmp[j];
    }
    return res;
}

int main(){
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin>>n;
    for(int i = 0; i < n; i++)
        cin>>q[i];

    cout<<merge_sort(0, n-1)<<endl;
}

二分

整数二分

![[Pasted image 20241114170240.png]]

本质：给定一个区间，存在某种性质，使得这个区间中的一部分满足，另一部分不满足，那么二分就可以寻找这两部分的边界
如果我们要找红色区间的右侧边界点：
1. 首先，设mid = (l + r + 1)/2
2. 其次检查mid是否符合红色区间的性质
  - 如果符合，那么红色区间边界点就位于[mid, r]之间；更新方式：l = mid
  - 如果不符合，那么红色区间边界点就位于[l, mid-1]之间；更新方式：r = mid - 1
如果我们要找绿色区间的左侧边界点：
1. 首先，设mid = (l + r)/2
2. 其次检查mid是否符合绿色区间的性质：
  - 如果符合，那么绿色区间边界点就位于[l, mid]之间；更新方式：r = mid
  - 如果不符合，那么红色区间边界点就位于[mid + 1, r]之间；更新方式：l = mid + 1

为什么要取1

不加会造成死循环

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 100;

int n, m;
int q[N];

int main(){
	std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 0; i < n; i++){
		cin >> q[i];
	}

	while(m--){
		int l = 0, r = n - 1;
		int x;
		cin >> x;
		//输入想要确定范围的数x
		int l = 0, r = n - 1;
		while(l < r){
			int mid = (l + r) / 2;
			if(q[mid] >= x)
				r = mid;
			else
				l = mid + 1;
		}


		if (q[l] != x)
			cout << "-1 -1" << endl;
		else{
			cout << l << " ";
			l = 0, r = n - 1;
			while(l < r){
				int mid = (l + r + 1) / 2;
				if(q[mid] <= x){
					l = mid;
				}
				else{
					r = mid - 1;
				}
			}
			cout << l << endl;
		}

	}



	return 0;
}

数的三次方根

代码

#include <bits/stdc++.h>
using namespace std;

int main(){
	double x;
	cin >> x;
	double l = - 10000, r = 10000;
	while(r - l < 1e-8){
		int mid = (l + r) / 2;
		if(mid * mid * mid >= x){
			r = mid;
		}
		else
			l  = mid;
	}

	printf("%lf", l);
	return 0;
}

高精度加法

如何存储大整数

将每一位存到一个数组里面
数组中的第一个位置（下标为0）的地方存个位
- 利于加法进位，如果最高位有进位的话，直接在数组末尾加一个数字即可

运算

A + B + t

代码

#include <bits/stdc++.h>
#include <vector>
using namespace std;

const int N = 1e6 + 100;

vector<int> add(vector<int> &A, vector<int> &B){
    vector<int> C;

    int t = 0;

    for(int i = 0; i < A.size()|| i < B.size(); i ++){
        if(i < A.size())  t += A[i];
        if(i < B.size())  t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if(t) C.push_back(1);
    return C;
}

int main(){
    // std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    string a, b;
    vector<int> A, B;

    cin >> a >> b;
    // 注意这里是字符串的size！！！
    for(int i = a.size() - 1; i >= 0; i --)  A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i --)  B.push_back(b[i] - '0');

    auto C = add(A, B);

    for(int i = C.size() - 1; i >= 0; i --)
        printf("%d", C[i]);


    return 0;
}

高精度减法

思想

假设被减数为 $A_3, A_2, A_1, A_0$，减数为$B_2, B_1, B_0$
分为两种情况进行分析
- 如果$A_i - B_i - t \geq 0$，那么直接进行减法，该数位的结果即为$A_i - B_i - t$
- 如果$A_i - B_i - t < 0$，那么需要借一位进行减法，该数位的结果即为$10 + A_i - B_i - t$
- 其中t就是判断上一位有没有借位的变量，如果借位了，那么t为1；反之，t为0
减法的正负
- 如果A > B，计算A - B
- 如果A < B，计算B - A

高精度减法

解题思路

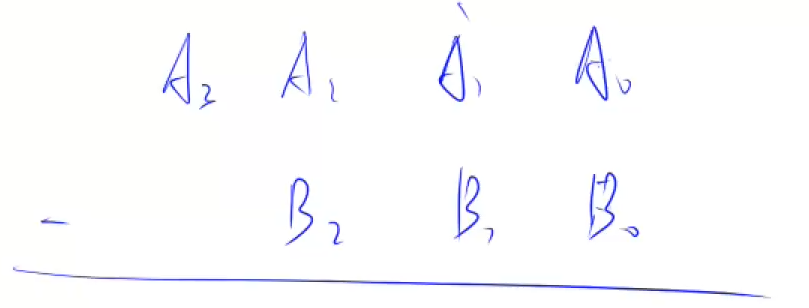
对于减法中每一位的运算，我们可以设被减数该位为$A_i$，减数该位为$B_i$，上一位的借位为$t$，那么将分为以下两种情况
- 如果$A_i - B_i - t >= 0$，那么该位运算结果为$A_i - B_i - t$
- 如果$A_i - B_i - t < 0$，那么该位运算结果为$10 + A_i - B_i - t$
对于减法的整体运算，设被减数为$A$，减数为$B$
- 如果$A - B \geq 0$，直接计算$A - B$
- 如果$A - B < 0$，则计算$B - A$
感觉本题的主要难度在模拟减法的过程

实现代码

#include <bits/stdc++.h>

using namespace std;

bool cmp(vector<int> &A, vector<int> &B){
    // 判断A >= B?
    if(A.size() != B.size())
        return A.size() > B.size();
    for(int i = A.size() - 1; i >= 0; i --){
        if(A[i] != B[i]){
            return A[i] > B[i];
        }
    }
    // 如果都一样，那么返回true
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B){
    vector<int> c;

    for(int i = 0, t = 0; i < A.size(); i ++){
        t = A[i] - t;
        if(i < B.size())
            t -= B[i];

        c.push_back((t + 10) % 10);

        if(t < 0)
            t = 1;
        else
            t = 0;
    }

    while(c.size() > 1 && c.back() == 0)
        c.pop_back();


    return c;
}


int main(){
    string a, b;
    vector<int> A, B;

    cin >> a >> b;

    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    for(int i = b.size() - 1; i >= 0; i --)
        B.push_back(b[i] - '0');

    if(cmp(A, B)){
        auto c = sub(A, B);

        for(int i = c.size() - 1; i >= 0; i --){
            cout << c[i];
        }
    }else{
        auto c = sub(B, A);

        cout << "-";
        for(int i = c.size() - 1; i >= 0; i --){
            cout << c[i];
        }
    }

    return 0;
}

高精度乘法

解题思路

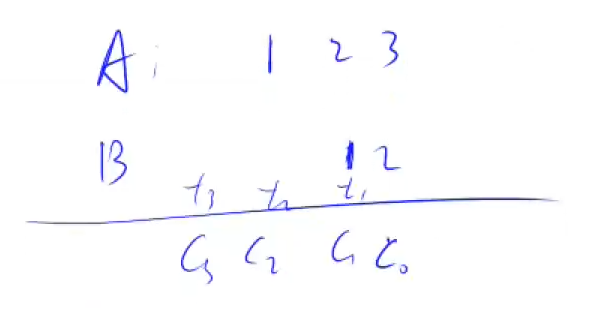
$C_0 = (3\times 12) \% 10, t_1 = (3\times 12) $\$ 10$
$C_1 = (2\times 12 + t_1) \% 10$, …

实现代码

#include <bits/stdc++.h>

using namespace std;

vector<int> mul(vector<int> &A, int b){

    vector<int> c;

    int t = 0;
    for(int i = 0; i < A.size() || t; i ++){
        if(i < A.size())
            t += A[i] *b;

        c.push_back(t % 10);
        t /= 10;
    }
    while(c.size() > 1 && c.back() == 0){
        c.pop_back();
    }
    return c;
}

int main(){
    string a;
    int b;

    cin >> a >> b;
    vector<int> A;


    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    auto c = mul(A, b);



    for(int i = c.size() - 1; i >= 0; i --)
        cout << c[i];

    return 0;
}

高精度除法

实现代码

#include <bits/stdc++.h>

using namespace std;

vector<int> div(vector<int> &A, int b, int &r){
    vector<int> c;
    r = 0;
    for(int i = A.size() - 1; i >= 0; i --){
        r = r * 10 + A[i];
        c.push_back(r / b);
        r %= b;
    }

    reverse(c.begin(), c.end());


    while(c.size() > 1 && c.back() == 0){
        c.pop_back();
    }

    return c;
}

int main(){
    string a;
    int b;

    cin >> a >> b;
    vector<int> A;


    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    int r;
    auto c = div(A, b, r);



    for(int i = c.size() - 1; i >= 0; i --)
        cout << c[i];

    cout << endl << r << endl;

    return 0;
}

前缀和

算法思想

有一个长度为$n$的数组，元素为$a_1, a_2, a_3, …, a_n$
前缀和数组则为$S_1, S_2, S_3, …, S_n$，其中$S_i = a_1 + a_2+a_3+…+a_i$
在前缀和中，一定要让数组的下标从1开始
如何求$S_i$

	for(int i = 1; i <= n; i ++){
		s[i] = s[i - 1] + a[i];
	}

$S_i$如何用
- 能够快速求出来数组中一段数的和
- 例如求[l, r]这段数的和，那么就可以通过$S_r - S_{l-1 }$来计算

代码实现

#include <bits/stdc++.h>

using namespace std;


const int N = 1e5 + 100;
int n, m;
int a[N], s[N];

int main(void){

    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
    }

    for(int i = 1; i <= n; i ++){
        s[i] = s[i - 1] + a[i];
    }

    while(m --){
        int l, r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

子矩阵的和

算法思想

s[i, j]表示的是：以位于第i行，第j列的小格子为右下顶点，构成的子矩阵中所有小格子中数字的和 ![[Pasted image 20250106152359.png]]
s[i, j]该如何计算呢？
- s[i, j] = s[i - 1, j] + s[i, j - 1] - s[i - 1, j - 1] + a[i][j]
给定坐标$(x_1, y_1), (x_2, y_2)$，以$(x_1, y_1)$为左上角，以$(x_2, y_2)$右下角的矩阵中所有数的和怎么求？
- 面积等于s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

代码实现

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;

int n, m;
int q;
int a[N][N], s[N][N];

int main(void){

    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m >> q;
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            cin >> a[i][j];
        }
    }

    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    int x1, y1, x2, y2;

    while(q --){
        cin >> x1 >> y1 >> x2 >> y2;

        cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;
    }


    return 0;
}

差分

算法思想

前缀和的逆运算
给定数组$a_1, a_2, a_3, a_4, …, a_n$
构造数组$b_1, b_2, b_3, … , b_n$
使得$a_i = b_1 +b_2 +b_3 + … + b_i$
那么b数组就称为a数组的差分
- 其中，b[2] = a[2] - a[1]
a数组就成为b数组的前缀和
现在让将数组a序列[l,r]中的数，每一个数都加上c
- 那么我们就可以让b[l]加上一个常数c
- 这样做之后，就可以让a[l] ~ a[n]都加上了c
- 但是我们不能让a[r]之后的数加上c
- 所以我们让b[r + 1] - c就ok啦
在初始化的时候：
- 可以先假定数组b都为0，然后我们让[i , i]区间中调用insert函数（自建的）insert(i, i, a[i])，这样就获得了初始化的数组b

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int n, m;
int a[N], b[N];

void insert(int l, int r, int c){
    b[l] += c;
    b[r + 1] -= c;
}

int main(void){


    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m;

    for(int i = 1; i <= n; i ++){
        cin >> a[i];
    }

    for(int i = 1; i <= n; i ++){
        insert(i, i, a[i]);
    }

    int l, r, c;

    while(m --){
        cin >> l >> r >> c;
        insert(l, r, c);
    }

    for(int i = 1; i <= n; i ++){
        b[i] += b[i - 1];
        cout << b[i] << " ";
        // 根据insert函数的定义，b[i - 1] 是等于 a[i - 1]的
    }

    cout << endl;

    return 0;
}

算法思想

假设有一个矩阵$a_{ij}$为原矩阵
构造差分矩阵$b_{ij}$
为原矩阵构造差分矩阵

为指定区域内的数组加上c

给定$(x_1, y_1), (x_2, y_2)$，为这个区域内的数字加上c（假设这些数字都是$a_{ij}$）
需要对差分矩阵中的元素进行下列的一些列操作
- $b_{(x_1,y_1)}$ += c
- $b_{(x_2 + 1,y_1)}$ -=c
- $b_{(x_1,y_2 + 1)}$ -=c
- $b_{(x_2,y_2)}$ += c
将上面的四个操作封装成一个函数
- 这个函数的作用：对b数组执行函数，等价于对a数组$(x_1, y_1), (x_2, y_2)$构成的矩形之间的元素都加上了c
- 这个函数可以用来初始化差分矩阵b

代码实现

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int a[N][N], b[N][N];
int n, m, q;

void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}


int main(void){
    cin >> n >> m >> q;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> a[i][j];


    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            insert(i, j, i, j, a[i][j]);
        }
    }

    int x1, y1, x2, y2, c;

    while(q --){
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            cout << b[i][j] << " ";
        }

        cout << endl;
    }


    return 0;
}

最长连续不重复子序列

解题思路

双指针算法的样子

for(int i = 0, j = 0; i < n; i ++){
	while(j < i && check(i, j)) j ++;
	// 每道题的具体逻辑
}

最核心的性质：可以优化

核心思想

for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++)
		//代码实现的逻辑
}

可以将$\Omega(n^2)$的朴素算法优化到$\Omega(n)$

最长连续不重复子序列

给定绿色右侧指针为当前的j（对于j的定义为：j往左能到的符合条件的、最远的地方），绿色左侧指针为假设我们还有一个j能更加左，但是这个与j的定义相矛盾，所以我们说j到i之间的距离就是最长连续不重复子序列的长度
基本代码模版为：

// 朴素做法，复杂度为O(n)
for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++){
		if(check(i, j)){
			res = max(res, i - j + 1);
		}
	}
}
// 双指针算法
// 发现一些单调性质，并利用
for(int i = 0; i < n; i ++){
	while(j <= i && check(i, j)){
		j ++;
	}

	res = max(res, i - j + 1);

}

代码实现

双指针算法最基本的应用

提取用空格分隔开的单词

#include <bits/stdc++.h>

using namespace std;

int main(){
	char str[100];
	gets(str);
//	这里一定要使用gets()，使用cin会导致第一个空格之后的字符没有被提取到
//	cout << str << endl;
//	cin 使用 >> 运算符的时候，默认会跳过空白字符，直到遇到下一个空白字符停止读取
// 	所以cin只能读取到第一个单词

	int n = strlen(str);

	for(int i = 0; i < n; i ++){
		int j = i;
		while(j < n && str[j] != ' '){

			j ++;

		}

		for(int k = i; k < j; k ++){
			cout << str[k];
//			注意 k ++ 这个语句是在一个循环块执行结束后执行
		}
		cout << endl;

		i = j;
	}


	return 0;

}

![[Pasted image 20250131121856.png]]

最长连续不重复子序列

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 100;
int n;
int a[N], s[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }

    int res = 0;
    for(int i = 0, j = 0; i < n; i ++){
        s[a[i]] ++;
        while(s[a[i]] > 1){
            s[a[j]] --;
            j ++;
        }

        res = max(res,i - j + 1);
    }


    cout << res << endl;

    return 0;
}

最长连续不重复子序列

解题思路

双指针算法的样子

for(int i = 0, j = 0; i < n; i ++){
	while(j < i && check(i, j)) j ++;
	// 每道题的具体逻辑
}

最核心的性质：可以优化

核心思想

for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++)
		//代码实现的逻辑
}

可以将$\Omega(n^2)$的朴素算法优化到$\Omega(n)$

最长连续不重复子序列

给定绿色右侧指针为当前的j（对于j的定义为：j往左能到的符合条件的、最远的地方），绿色左侧指针为假设我们还有一个j能更加左，但是这个与j的定义相矛盾，所以我们说j到i之间的距离就是最长连续不重复子序列的长度
基本代码模版为：

// 朴素做法，复杂度为O(n)
for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++){
		if(check(i, j)){
			res = max(res, i - j + 1);
		}
	}
}
// 双指针算法
// 发现一些单调性质，并利用
for(int i = 0; i < n; i ++){
	while(j <= i && check(i, j)){
		j ++;
	}

	res = max(res, i - j + 1);

}

代码实现

双指针算法最基本的应用

提取用空格分隔开的单词

#include <bits/stdc++.h>

using namespace std;

int main(){
	char str[100];
	gets(str);
//	这里一定要使用gets()，使用cin会导致第一个空格之后的字符没有被提取到
//	cout << str << endl;
//	cin 使用 >> 运算符的时候，默认会跳过空白字符，直到遇到下一个空白字符停止读取
// 	所以cin只能读取到第一个单词

	int n = strlen(str);

	for(int i = 0; i < n; i ++){
		int j = i;
		while(j < n && str[j] != ' '){

			j ++;

		}

		for(int k = i; k < j; k ++){
			cout << str[k];
//			注意 k ++ 这个语句是在一个循环块执行结束后执行
		}
		cout << endl;

		i = j;
	}


	return 0;

}

![[Pasted image 20250131121856.png]]

最长连续不重复子序列

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 100;
int n;
int a[N], s[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }

    int res = 0;
    for(int i = 0, j = 0; i < n; i ++){
        s[a[i]] ++;
        while(s[a[i]] > 1){
            s[a[j]] --;
            j ++;
        }

        res = max(res,i - j + 1);
    }


    cout << res << endl;

    return 0;
}

数组元素的目标和

实现思想

暴力做法（容易超时）
找单调性：
- 主要思路是for(int i = 0; i < n; i ++)，找到一个j，使得$A_i+B_j\geq x$，同时j的下标是最小的
- 当有满足条件的下标i, j出现的时候，直接输出答案并break

实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 100;
int n, m, x;
int a[N], b[N];

int main(){
    cin >> n >> m >> x;
    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }
    for(int i = 0; i < m; i ++){
        cin >> b[i];
    }

    for(int i = 0, j = m - 1; i < n; i ++){

        while(j >= 0 && a[i] + b[j] > x){
            j --;
        }
        if(a[i] + b[j] == x){
            cout << i << " " << j << endl;
            break;
        }
    }
}

判断子序列

解题思路

对数组B中的每一个元素进行遍历，如果出现了一个数组A中的元素相同的元素（第一个），就将其与数组A中的映射关系记录下来
如果遍历完数组B，数组A中的每个元素都找到了，那么我们可以说数组B中存在一个数组A的子序列的匹配
下面我们需要证明，如果数组B存在着数组A的子序列，那么上述算法一定可以找出一种匹配
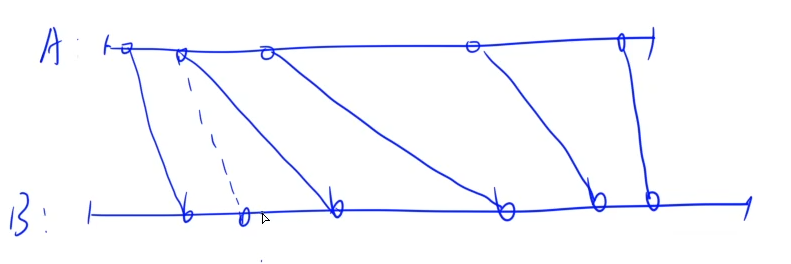
- 假定数组B中存在着一组匹配，我们遍历数组A的每个元素，在数组B中寻找与之匹配的元素
- 如果找到了一个与数组A中元素相同，但是这个元素位于匹配中对应元素之前，如上图虚线所示（实线为假定的匹配）。
- 我们可以将实线的匹配，替换为虚线的匹配。这样做我们发现，这其实是不会影响后续的匹配的，即说明，使用双指针算法可以找到存在的合法匹配。
在这种类似于“贪心”的算法中，证明充分必要性是很重要的，在本题中：
- 充分性：如果双指针算法找到了一个匹配，那么这确实是一个合法的子序列匹配
- 必要性：如果存在一个合法的子序列匹配，那么双指针算法一定能够找到一个合法的匹配
- 证明必要性的原因：通过证明必要性，即使存在其他的匹配，我们也可以证明即使是“贪心”地选择了第一个（相对地）匹配的元素，那么形成的匹配也是合法的。

实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 100;
int a[N], b[N];
int n, m;

int main(){
    cin >> n >> m;

    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }

    for(int i = 0; i < m; i ++){
        cin >> b[i];
    }

    int i = 0, j = 0;
    while(i < n && j < m){
        if(a[i] == b[j]){
            i ++;
        }
        j ++;
    }
    if(i == n){
        cout << "Yes" << endl;
    }else{
        cout << "No" << endl;
    }

    return 0;

}

n的二进制表示中第k位是几

知识点

按位与运算符

&位运算符
- 用于两个数字之间时，&运算符会将两个数字的二进制表示进行逐位与运算
- 运算规则为：只有当两个位都为1时，结果才为1，否则为0

计算机语言中的各种码

给定$(x)_2 = 1010$，x为32位整数
原码：0000 … 1010
反码：1111 … 0101
补码：1111 … 0110 (取反加一)

假设n = 6
n的二进制表示为0110
1的二进制表示为0001
那么n & 1的结果为0000

解题思路

求数字n的第k位，就将数字n右移k位并
- 先把第k位移动到最后1位
- 并把移动后的个位数 &1

实现代码

#include <bits/stdc++.h>
using namespace std;

int main(){
	int n = 10;

	for(int k = 3; k >= 0; k --){
		cout << (n >> k & 1);
	}
	return 0;
}

lowbit 操作

返回x的最后一位1，并且是一个二进制数
- 如果$(x)_2 = 1010$，那么lowbit(x) = 10
- 如果$(x)_2 = 101000$，那么lowbit(x) = 1000

实现原理

x & -x
在c++中，-x的二进制表示与~x + 1的二进制表示是相同的，其中~x是x的补码

           x = 1010 ... 100 ... 0
          ~x = 0101 ... 011 ... 1
      ~x + 1 = 0101 ... 100 ... 0
x & (~x + 1) = 0000 ... 100 ... 0

可以看到，x & (~x + 1)的结果返回的就是最后一位1的二进制数

二进制中1的个数

解题思路

通过多次lowbit操作，找到数字二进制中1的个数。每次进行玩lowbit操作，都会将最后1位1减去，实现数字的更新

实现代码

#include <bits/stdc++.h>

using namespace std;

int lowbit(int x){
    return x & -x;
}

int main(){
    int n;
    cin >> n;

    while(n --){
        int x;
        cin >> x;

        int cnt = 0;
        while(x){
            x -= lowbit(x);
            cnt ++;
        }


        cout << cnt << " ";
    }

    return 0;
}

离散化

1, 3, 5, ..., 1e9

有几个数字，数值的范围特别大，但是个数比较少。
有时候需要将数值特别大的数字作为下标使用，但是由于数值特别大，我们的存储空间无法满足要求
所以我们要将这几个数字与连续的自然数建立映射
这个就叫做离散化

a[]	1	3	5	100000	50000000
n	0	1	2	3	4

存在的问题

a[]中可能有重复的元素，需要去重
如何算出x离散化后的值

解决问题

去重

在c++中，我们有一个专用的套路去除vector中的所有元素

vector<int> alls;
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());

解题思路

目前给定的数轴太长了，数据范围是[-1e9, 1e9]
经过我们的分析，在这个数轴上，我们最多最多只能用到$3\times 1e5$个数
所以我们要将这$3\times 1e5$的下标，排序后映射到从1开始的自然数
假设下标映射后为k，那么我们让a[k] += c

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 3 * 1e5 + 100;

typedef pair<int, int> PII;

int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x){
    // 这个二分find的目的是找到数字插入的位置
    int l = 0, r = alls.size() - 1;
    while(l < r){
        int mid = (l + r) / 2;

        if(alls[mid] >= x)
        // 这里需要研究一下
            r = mid;
        else
            l = mid + 1;
    }

    return r + 1;
}

int main(void){
    cin >> n >> m;

    for(int i = 0; i< n; i ++){
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }

    for(int i = 0; i < m; i ++){
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }


    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());


    for(auto item: add){
        int x = find(item.first);
        a[x] += item.second;
    }

    for(int i = 0; i <= alls.size(); i ++){
        s[i] = s[i - 1] + a[i];
    }

    for(auto item: query){
        int l = find(item.first);
        int r = find(item.second);

        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

区间合并

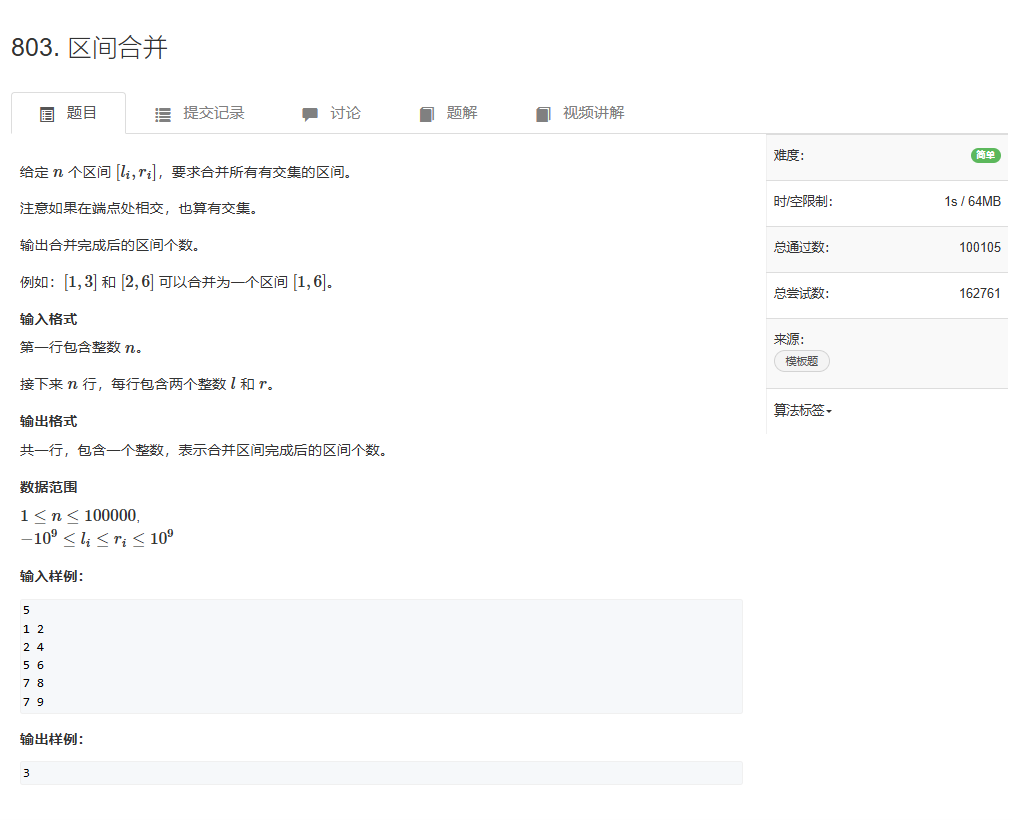
用例演示

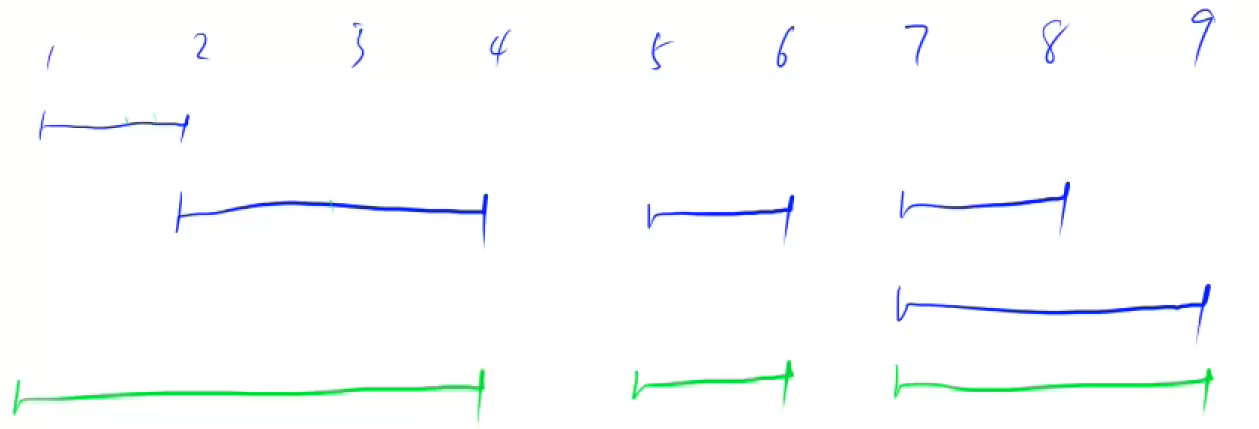
多个蓝色小区间可以合并为三个绿色区间

解题思路

情况1：无需改变当前区间
情况2：将当前区间的end向后延伸
情况3：当前区间的任务已经完成，可以将当前区间放入答案集中，并将原区间start和end更新为粉色区间的start和end

实现代码

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e5 + 100;

int n;
vector<PII> segs;

void merge(vector<PII> &segs){
    vector<PII> res;


    sort(segs.begin(), segs.end());

    int start = -2e9, end = -2e9;
    // 注意这里end也是-2e9，因为是从左边来的，不能是2e9,否则就比不了啦！
    for(auto seg: segs){
        if(end < seg.first){
            if(start != -2e9){
                res.push_back({start, end});
            }
            start = seg.first, end= seg.second;

        }else{
            end = max(end, seg.second);
        }
    }

    // 将最后一段合并区间也放入答案中
    if(start != -2e9)
        res.push_back({start, end});

    segs = res;
}

int main(){
    cin >> n;

    for(int i = 0; i < n; i ++){
        int l, r;
        cin >> l >> r;

        segs.push_back({l, r});
    }

    merge(segs);

    cout << segs.size() << endl;

    return 0;

}