高精度减法

解题思路

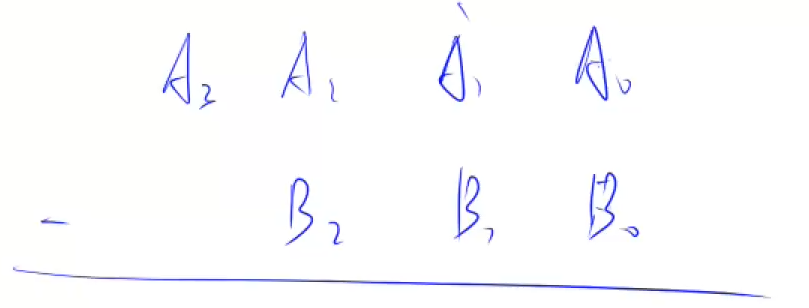
对于减法中每一位的运算，我们可以设被减数该位为$A_i$，减数该位为$B_i$，上一位的借位为$t$，那么将分为以下两种情况
- 如果$A_i - B_i - t >= 0$，那么该位运算结果为$A_i - B_i - t$
- 如果$A_i - B_i - t < 0$，那么该位运算结果为$10 + A_i - B_i - t$
对于减法的整体运算，设被减数为$A$，减数为$B$
- 如果$A - B \geq 0$，直接计算$A - B$
- 如果$A - B < 0$，则计算$B - A$
感觉本题的主要难度在模拟减法的过程

实现代码

#include <bits/stdc++.h>

using namespace std;

bool cmp(vector<int> &A, vector<int> &B){
    // 判断A >= B?
    if(A.size() != B.size())
        return A.size() > B.size();
    for(int i = A.size() - 1; i >= 0; i --){
        if(A[i] != B[i]){
            return A[i] > B[i];
        }
    }
    // 如果都一样，那么返回true
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B){
    vector<int> c;

    for(int i = 0, t = 0; i < A.size(); i ++){
        t = A[i] - t;
        if(i < B.size())
            t -= B[i];

        c.push_back((t + 10) % 10);

        if(t < 0)
            t = 1;
        else
            t = 0;
    }

    while(c.size() > 1 && c.back() == 0)
        c.pop_back();


    return c;
}


int main(){
    string a, b;
    vector<int> A, B;

    cin >> a >> b;

    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    for(int i = b.size() - 1; i >= 0; i --)
        B.push_back(b[i] - '0');

    if(cmp(A, B)){
        auto c = sub(A, B);

        for(int i = c.size() - 1; i >= 0; i --){
            cout << c[i];
        }
    }else{
        auto c = sub(B, A);

        cout << "-";
        for(int i = c.size() - 1; i >= 0; i --){
            cout << c[i];
        }
    }

    return 0;
}

高精度乘法

解题思路

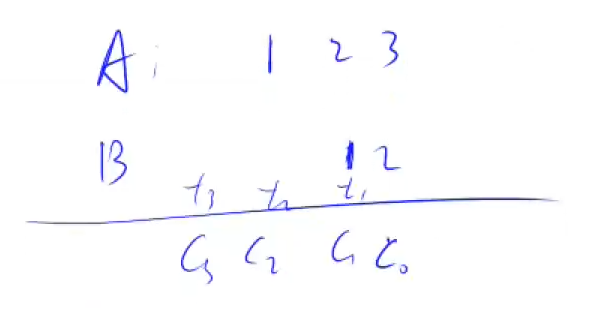
$C_0 = (3\times 12) \% 10, t_1 = (3\times 12) $\$ 10$
$C_1 = (2\times 12 + t_1) \% 10$, …

实现代码

#include <bits/stdc++.h>

using namespace std;

vector<int> mul(vector<int> &A, int b){

    vector<int> c;

    int t = 0;
    for(int i = 0; i < A.size() || t; i ++){
        if(i < A.size())
            t += A[i] *b;

        c.push_back(t % 10);
        t /= 10;
    }
    while(c.size() > 1 && c.back() == 0){
        c.pop_back();
    }
    return c;
}

int main(){
    string a;
    int b;

    cin >> a >> b;
    vector<int> A;


    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    auto c = mul(A, b);



    for(int i = c.size() - 1; i >= 0; i --)
        cout << c[i];

    return 0;
}

高精度除法

实现代码

#include <bits/stdc++.h>

using namespace std;

vector<int> div(vector<int> &A, int b, int &r){
    vector<int> c;
    r = 0;
    for(int i = A.size() - 1; i >= 0; i --){
        r = r * 10 + A[i];
        c.push_back(r / b);
        r %= b;
    }

    reverse(c.begin(), c.end());


    while(c.size() > 1 && c.back() == 0){
        c.pop_back();
    }

    return c;
}

int main(){
    string a;
    int b;

    cin >> a >> b;
    vector<int> A;


    for(int i = a.size() - 1; i >= 0; i --)
        A.push_back(a[i] - '0');

    int r;
    auto c = div(A, b, r);



    for(int i = c.size() - 1; i >= 0; i --)
        cout << c[i];

    cout << endl << r << endl;

    return 0;
}

高精度减法

解题思路

实现代码

高精度乘法

解题思路

实现代码

高精度除法

实现代码

Enjoy Reading This Article?