面试总结

• 五一前的一场面试给我拷打够呛，完成面试之后整个人坐在椅子上感觉浑身乏力（后来发现是tm要感冒，五一光吃药了），对五一假期的到来也不那么高兴。
• 仔细想了一下，被拷打是一件好事，总要比保研面试时被拷打住要好得多，更能明确自己的不足，持续进步。
• 于是开始记录一下自己被拷打住的地方，弥补自己的不足
• 平时如果自己看到简历中有哪些地方，也在这里记录上
• 大致从两个方面记录：
  • 专业课
  • 项目

2025.04.30

专业课

• 提到了人工智能技术、自然语言处理这两门课程
• 问：那你说说这个模型是怎么预训练的呢？（我提到了我在课设中应用了BLIP模型）
  • 答：我直接从huggingface上下载的模型参数，没进行预训练

• 正确解答：

  • 因为我主要展示的是基于图片生成字幕的功能，所以聚焦于image_grounded text decoder
• 问：讲一下反向传播吧
  • 答：讲的比较含糊
• 正确回答：
  • 损失函数归根到底是关于权重和bias的函数，所以我们通过链式法则就能获取到每个权重的梯度变化应该是多少

\[\frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C0}{\partial a^{(L)}}\]

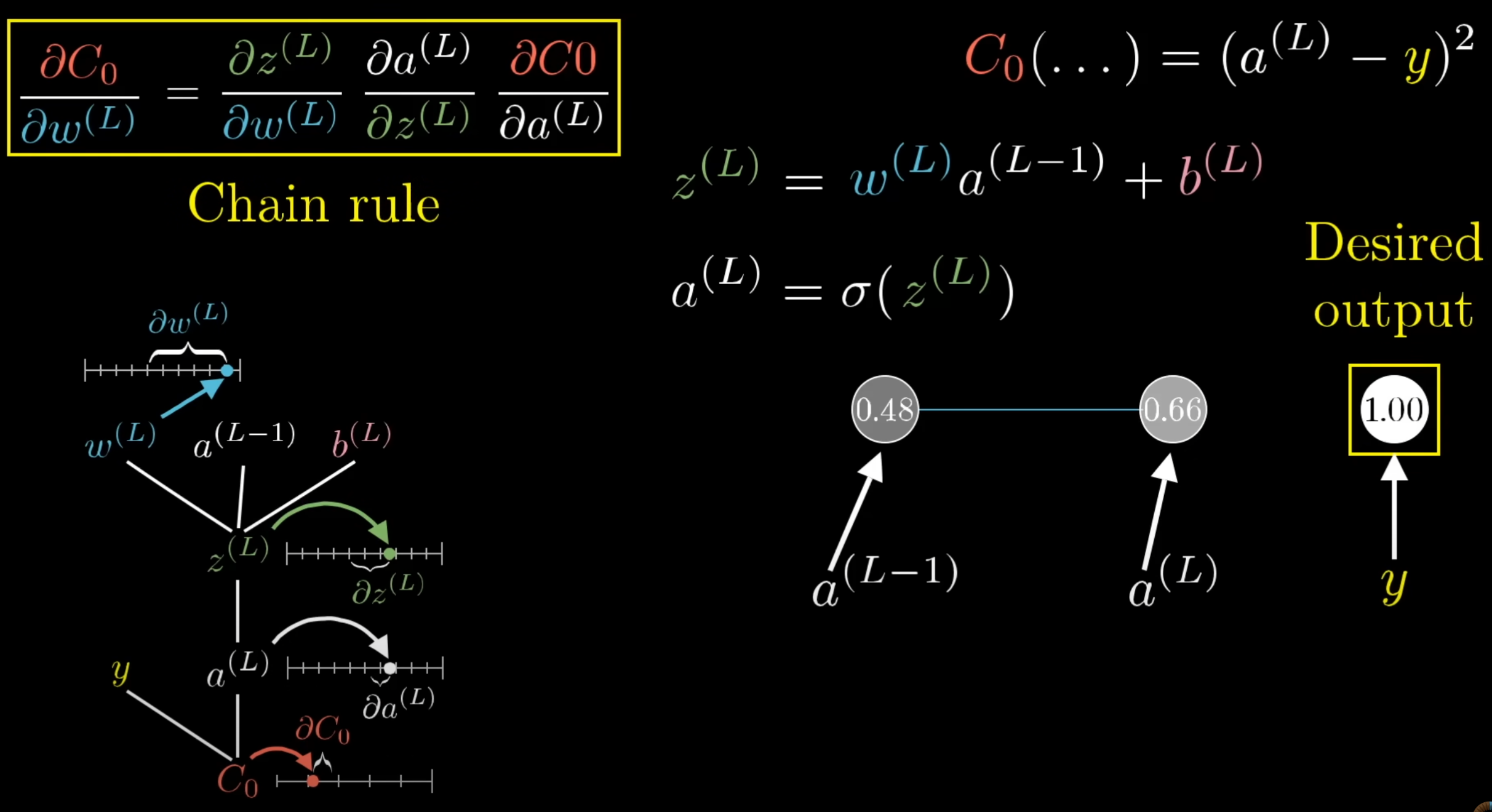
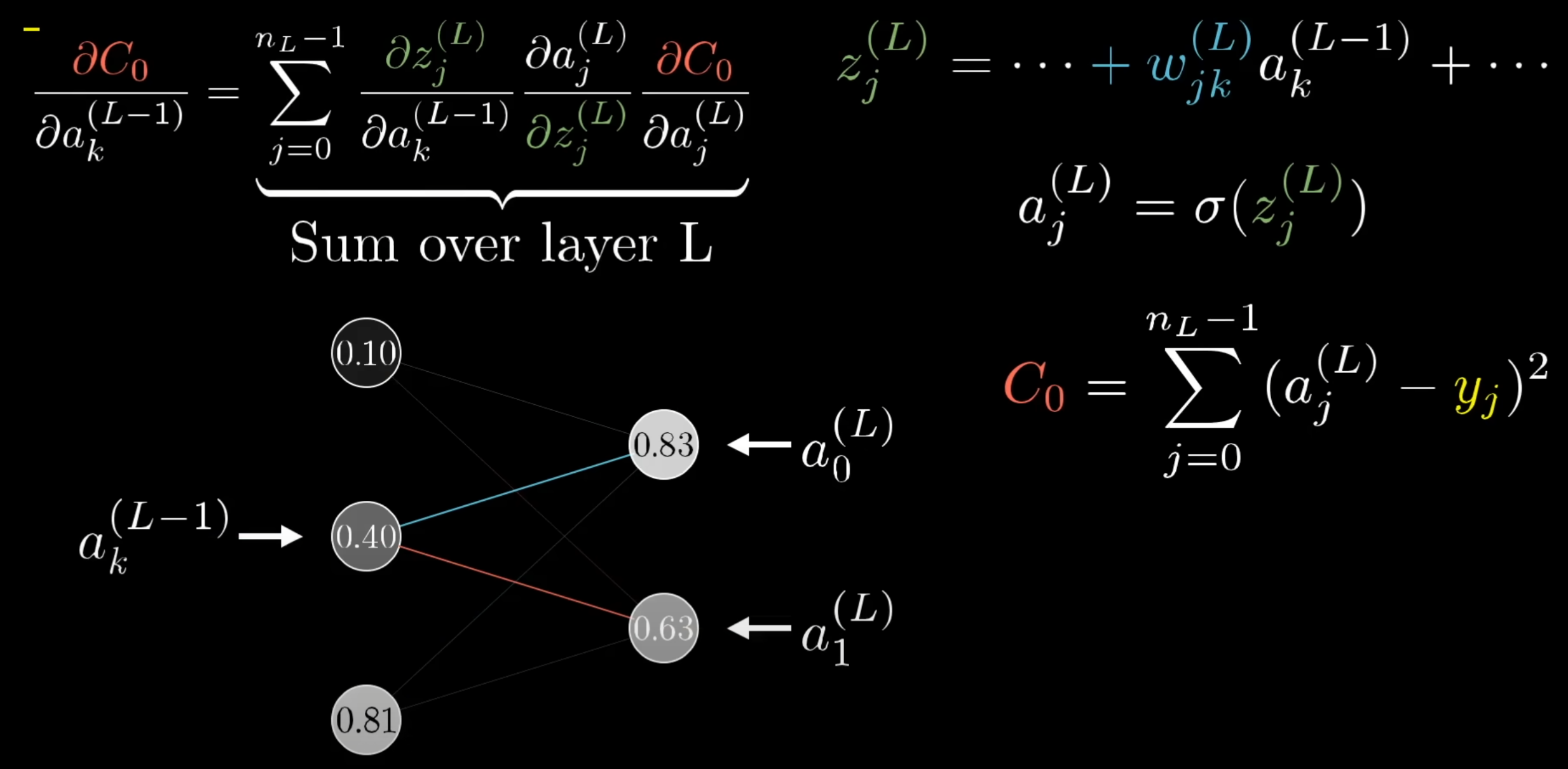
• 可以看到损失函数对任意一层的权重或者偏置的梯度，都可以通过损失函数对最后一层激活（输出）的导数，激活对于上一层线性加和的导数（非线性激活函数的导数），线性加和对上一层的导数逐层求得
• 获得了梯度，我们还需要设置一定的学习率
• 学习率乘以梯度，就是我们每个权重在每轮次训练中需要变化的值

反向传播知识总结

基本原理

• 反向传播是神经网络训练的核心算法，用于计算损失函数对网络中每个参数的梯度
• 基于链式法则，从输出层向输入层逐层计算梯度
• 目标是最小化损失函数，通过梯度下降调整网络参数

计算步骤

1. 前向传播：计算每一层的输出和最终的损失值
2. 计算输出层梯度：损失函数对输出层的梯度
3. 反向传播梯度：利用链式法则逐层向后计算梯度
4. 更新参数：根据计算得到的梯度和学习率更新权重和偏置

数学表达

• 对于第$l$层的权重$w^{(l)}$，其梯度计算为： \(\frac{\partial C}{\partial w^{(l)}} = \frac{\partial C}{\partial a^{(l+1)}} \frac{\partial a^{(l+1)}}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial w^{(l)}}\)

• 其中：

  • $C$是损失函数
  • $a^{(l)}$是第$l$层的激活值
  • $z^{(l)}$是第$l$层的加权输入

常见问题与优化

• 梯度消失/爆炸：深层网络中梯度可能变得非常小或非常大
  • 解决方法：使用ReLU等激活函数、批归一化、残差连接

• 学习率选择：过大可能导致震荡，过小可能收敛太慢

  • 解决方法：学习率调度、自适应学习率算法(Adam, RMSprop)
• 和这部分有关的内容应该还有sft, autoregressive

项目

联邦学习课题组项目

• 问：给我讲一下整个论文的idea是什么样的
  • 答：记不太清了……
• 正确回答：要从这几个方面进行回答：问题背景、存在什么问题、你是怎么做的、问题是否得到解决、未来还能怎么扩展。
  • 问题背景：
    • 传统联邦学习假设每个参与者既拥有数据又具备计算能力，但是对于这两种资源的分离的情况处理的并不太好
    • 数据拥有者不愿意直接交易数据，而是更倾向于以“信息流通”的方式实现数据的价值
  • 存在什么问题：
    • 如何在数据和算力解耦的情况下实现FL(数据拥有者没有算力，算力拥有者没有数据)
    • 如何激励三方（数据所有者、计算中心、模型所有者）采取最优策略
    • 如何量化数据所有者对最终模型的贡献并制定合理的奖励机制
  • 怎么做的：
    • 资源解耦的FL框架：将参与者分为三方
      • 模型所有者
      • 数据所有者
      • 计算中心
    • 三方Stackelberg框架：
      • 构建了一个分层博弈结构
      • 模型所有者为领导者
      • 数据所有者为副领导者
      • 计算中心为追随者
      • 导出了三方的效用函数和Stackelberg-Nash均衡
    • QR-RDFL算法
      • 一种质量感知的动态优化算法
      • 根据数据质量和动态损失策略组合，鼓励高质量数据的参与
  • 问题是否的到解决：
    • 提高了数据所有者参与的积极性
    • 解决了数据质量和数量异质带来的不公平问题
    • 显著提升了全局模型的性能和三方效用
    • 验证了算法在多种数据集上的适应性与鲁棒性
• 问：给我讲解一下这个stackelberg game是什么
  • 答：
    • 我说的是一种层级结构，上面有一个领导者，下面有追随者
    • 领导者作出决定，追随者跟着决定来制定自己的最优策略
• 正确回答：
  • Stackelberg博弈（Stackelberg Game）是一种非合作博弈模型，由经济学家Heinrich von Stackelberg于1934年提出
  • 核心特点：
    • 博弈中存在明确的先后顺序，分为领导者（Leader）和追随者（Follower）
    • 领导者先行动，追随者观察领导者的行动后再做决策
    • 领导者在做决策时会考虑到追随者的最优反应函数
    • 最终达到的均衡称为Stackelberg均衡
  • 与Nash均衡的区别：
    • Nash均衡假设所有参与者同时行动
    • Stackelberg均衡考虑了行动的先后顺序
  • 例子：市场定价模型
    • 假设市场上有两家公司A和B生产同类产品
    • 公司A是市场领导者，先确定自己产品的价格
    • 公司B是追随者，观察A的价格后再决定自己的价格
    • 公司A在设定价格时，会预测公司B对其价格的最优反应
    • 公司A会选择能使自己利润最大化的价格，同时考虑到B的反应
    • 这种情况下的均衡价格和产量与两家公司同时定价的Nash均衡不同
  • 在联邦学习中的应用：
    • 服务器可以作为领导者，客户端作为追随者
    • 服务器先决定资源分配或激励机制
    • 客户端根据服务器的决策选择自己的最优参与策略
    • 这种框架有助于解决联邦学习中的激励机制设计问题

南洋理工大学交流项目

• 好像比较年轻的老师都爱问这段经历💭
• 问：你都用过哪些模型的api？
  • 答：我用过deepseek，MOONSHOT，gemini（免费）
• 问：你感觉这些模型中，谁的api比较好用？
  • 答：我感觉都差不多
• 正确回答：
• 问：如何保证你调用的api内容是相关的
  • 答：好像有一个参数叫做tempreture
• 正确回答：可以分为两个角度进行回答
  • 提示工程（prompt engineering）
    • 一些通用技巧
      • 指令：使用命令来指示模型执行各种简单任务，例如“写入”、“分类”、“总结”、“翻译”、“排序”等
      • 具体性：
        • 提取以下文本中的地名。
        • 所需格式：
        • **地点：<逗号分隔的公司名称列表>**逗号分隔的公司名称列表>
        • 输入：“虽然这些发展对研究人员来说是令人鼓舞的，但仍有许多谜团。里斯本未知的香帕利莫德中心的神经免疫学家 Henrique Veiga-Fernandes 说：“我们经常在大脑和我们在周围看到的效果之间有一个黑匣子。”“如果我们想在治疗背景下使用它，我们实际上需要了解机制。””
      • 避免不明确：
        • 解释提示工程的概念。保持解释简短，只有几句话，不要过于描述。
        • 使用 2-3 句话向高中学生解释提示工程的概念。
      • 做什么还是不做什么：
        • 以下是向客户推荐电影的代理程序。不要询问兴趣。不要询问个人信息。
        • 客户：请根据我的兴趣推荐电影
        • 代理：
    • 一些专业提示技术
      • 零样本提示
      • 少样本提示
      • CoT链式思考提示
  • api参数
    • tempreture:
      • tempreture越高，token的概率分布会更加的平坦，高概率token概率降低，低概率token概率升高，使得模型在选择下一个token时会更加随机
      • tempreture越低，token的概率分布会更加的陡峭，高概率token概率会更加升高，低概率token概率会更加降低，使得模型选择下一个token时，更倾向与选择高概率的token
    • top_p: top_p采样是指从最高概率（核心）token中进行选取。
      • 假设top_p为$\alpha$，则我们先将所有token出现的概率进行排序，从最高的概率的token开始对概率进行累加，直至和等于$\alpha$停止
      • 当top_p升高时，考虑的token越多
      • 当top_p降低时，考虑的toekn越少
    • tempreture和top_p越高，生成的文本更多样，反之生成的文本比较确定
      • 高：适合生成多样性的文本，例如创意写作，头脑风暴等场景
      • 低：适合生成确定性的文本，例如回答论述题、选择题，法律、科技专业用词查询等场景

剑桥大学交流项目

• 老师估计也是不知道问什么了，都问到我这部分经历了
• 问：给我讲一讲贝叶斯理论吧
  • 答：老师这个知识时间有点长了，我也忘了，就记得一些术语叫做qianjian（hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh）
  • 追问：你用英文说吧
  • 答：prior
• 正确回答：见下面
• 问：那贝叶斯理论中prior，likelihood，posterior都是什么
  • 答：没答上来……
• 正确回答：
  • **prior（先验概率）: **
    • 没给定条件时，单独观察事件A发生的概率;或者说是，我们先给定一种假设，观察到这种假设的概率是多少
    • 在贝叶斯理论中，先验概率表示在获得新数据之前，我们对某个参数或假设的初始信念或知识
    • 数学表示：P(A)，表示事件A发生的概率
    • 例子：在医学诊断中，某种疾病在总人口中的发病率（如1%）就是该疾病存在的先验概率
  • likelihood（似然概率）:
    • 给定一种证据，在假设的条件下，观察到这种证据的概率；
    • 维基百科：概率，用于在已知一些参数的情况下，预测接下来在观测上所得到的结果；似然性，则是用于在已知某些观测所得到的结果时，对有关事物之性质的参数进行估值，也就是说已观察到某事件后，对相关参数进行猜测。

    • 数学表示：**P(B

      A)，表示在事件A发生的条件下，事件B发生的概率**

    • 例子：如果一个人患有某种疾病（假设A），那么检测呈阳性（证据B）的概率是多少
  • posterior（后验概率）:
    • 在证据的条件下，发生这种假设的概率；猜测出来参数的值
    • 后验概率是贝叶斯定理的核心，它表示在观察到新证据后，我们对假设的更新信念

    • 数学表示：P(A

      B)，表示在观察到事件B后，事件A成立的概率

    • 例子：如果检测结果呈阳性，那么该人确实患有疾病的概率是多少

  • 贝叶斯公式：P(A

    B) = [P(B

    A) × P(A)] / P(B)

    • 这个公式将先验概率P(A)、似然概率P(B

      A)和后验概率P(A

      B)联系起来

    • P(B)是归一化常数，表示事件B发生的总概率
• 老师指出，梯度下降是一种优化方法，而贝叶斯理论是一种基础理论框架，两者属于不同层面的概念，不应混为一谈
  • 神经网络学习的本质是最小化损失函数的过程
  • 在任何维度的函数中，沿着梯度方向函数值增长最快，因此沿着梯度的反方向，函数值下降也最快
  • 梯度下降算法通过计算梯度来确定权重应该增加还是减少，以及具体的变化量大小
  • 在梯度下降优化过程中，我们特别关注那些对损失函数影响较大的权重参数，即投入产出比最高的参数调整（which one gets you most bang for a buck）
  • 由于使用全部样本计算梯度非常耗时，实践中常采用随机梯度下降（Stochastic Gradient Descent），将数据集分成多个小批量（mini-batch）进行训练，既提高效率又保持了优化效果