数据结构
单链表
用数组模拟单链表
邻接表
- 存储树和图
单链表
- 样式:
- head -> $\phi$
- head -> element -> element -> $\phi$
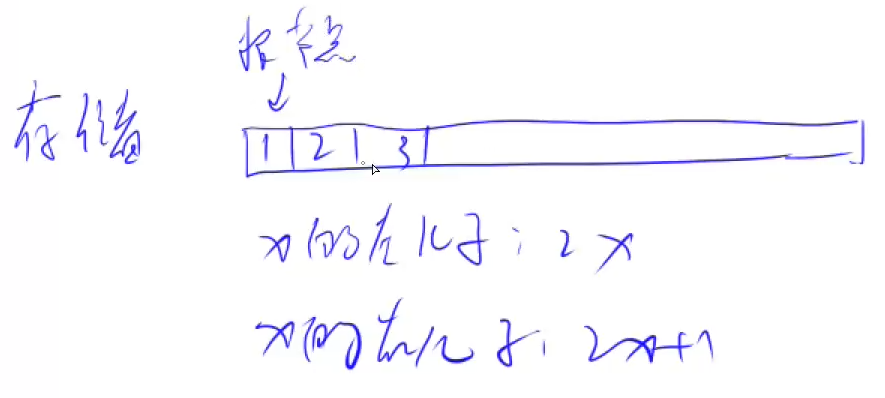
- 定义
- int e[N]:表示某个点的值是多少
- int ne[N]:表示下一个点的指针
- 两个数组用下标关联起来
- 空节点的下标用-1表示
- ![[Pasted image 20241216084447.png]]
一些函数操作
- 初始化
- 请注意,head不是一个结点,而是一个“指针”,head指向的是头结点的下标
void init(){
head = -1;
idx = 0;
}
- 在链表头部,插入一个新结点
- 操作步骤:
- 将新结点的next指针指向头结点的下一个结点
- 将新插入的结点的next指针指向头结点
- 操作步骤:
void add_to_head(int x){
e[idx] = x;
ne[idx] = head;
head = idx ++;
}
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
// head表示头结点的下标
// e[N]存储每个结点的值,表示结点i的值
// ne[N]表示结点i的next指针,即为下一个结点的下标值
// idx存储当前已经用到了哪个点
int head, e[N], ne[N], idx;
void init(){
head = -1;
idx = 0;
}
void add_to_head(int x){
e[idx] = x;
ne[idx] = head;
head = idx ++;
}
void add(int k, int x){
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx ++;
}
void remove(int k){
ne[k] = ne[ne[k]];
}
int main(){
int m;
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> m;
init();
while(m --){
char op;
int x, k;
cin >> op;
if(op == 'H'){
cin >> x;
add_to_head(x);
}
else if(op == 'D'){
cin >> k;
if(!k)
head = ne[head];
remove(k - 1);
}
else{
cin >> k >> x;
add(k - 1, x);
}
}
for(int i = head; i != -1; i = ne[i]){
cout << e[i] << ' ';
}
cout << endl;
return 0;
}
双链表
用数组模拟双链表
- 每个节点有两个指针
-
int l[N]存储左侧指针指向的下标,int r[N]存储右侧指针指向的下标
主要功能
初始化函数
- 用
0表示左节点,用1表示右节点 - 那么最开始双链表的情况就为
r[0] = 1, l[1] = 0
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
int m;
int e[N], l[N], r[N], idx;
void init(){
r[0] = 1, l[1] = 0;
idx = 2;
}
// 在下标时k节点的右边插入一个值为x的结点
void add(int k, int x){
e[idx] = x;
r[idx] = r[k];
l[idx] = k;
l[r[k]] = k;
r[k] = idx ++;
}
void remove(int k){
r[l[k]] = r[k];
l[r[k]] = l[k];
}
int main(){
cin >> m;
init();
while(m --){
string op;
int x, k;
cin >> op;
if(op == "R"){
cin >> x;
add(l[1], x);
// 这里的1表示的是右边界,在右边界左侧节点的右侧插入新结点
}
else if(op == "L"){
cin >> x;
add(0, x);
// 最开始在这里犯了错误,应该直接在0节点(头结点)的右侧进行插入的
// 0, 1都没有实际值,只是一个头尾指针
}
else if(op == "D"){
cin >> k;
remove(k + 1);
// 数组中的idx实际是从2开始算的,所以这里是k + 1
}
else if(op == "IL"){
cin >> k >> x;
add(l[k + 1], x);
}
else{
cin >> k >> x;
add(k + 1, x);
}
}
for(int i = r[0]; i != 1; i = r[i]){
cout << e[i] << " ";
}
cout << endl;
return 0;
}
栈
模拟栈
实现思想
- 先进后出
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int m;
int stk[N], tt;
int main(){
cin >> m;
while(m --){
string op;
int x;
cin >> op;
if(op == "push"){
cin >> x;
stk[++ tt] = x;
}
else if(op == "pop"){
tt --;
}
else if(op == "query"){
cout << stk[tt] << endl;
}
else{
cout << (tt ? "NO" : "YES") << endl;
}
}
return 0;
}
表达式求值
算法思想
- 利用中缀表达式模拟递归求解
- 如何判断一颗子树已经被遍历完?当前运算符的优先级小于等于上一运算符的优先级
实现代码
#include <bits/stdc++.h>
using namespace std;
stack<int> num;
stack<char> op;
unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
void eval(){
int b = num.top();
num.pop();
int a = num.top();
num.pop();
int c = op.top();
op.pop();
int r = 0;
if(c == '+') r = a + b;
else if (c == '-') r = a - b;
else if (c == '*') r = a * b;
else r = a / b;
num.push(r);
}
int main(){
string s;
// 读入表达式
cin >> s;
for(int i = 0; i < s.size(); i ++){
// 开始遍历表达式
if(isdigit(s[i])){
int x = 0, j = i;
while(j < s.size() && isdigit(s[j])){
x = x * 10 + s[j] - '0';
j ++;
}
i = j - 1;
num.push(x);
}
else if(s[i] == '('){
op.push(s[i]);
}
else if(s[i] == ')'){
// 干脆就没让右括号进栈
while(op.top() != '('){
eval();
}
op.pop();
}
else{
while(op.size() && h[op.top()] >= h[s[i]]){
eval();
}
op.push(s[i]);
}
}
while(op.size()) eval();
cout << num.top() << endl;
return 0;
}
队列
模拟队列
解题思路
- 用数组模拟队列
- 初始化数组,
hh = 0表示对头,tt = -1表示队尾 - 在队尾插入元素,在队头弹出元素
- 插入元素:
q[++ tt] = x - 弹出元素:
hh ++ - 取出队头元素:
q[hh] - 取出队尾元素:
q[tt]
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
int q[N], hh, tt = -1;
int main(){
int m;
scanf("%d", &m);
while(m --){
string s;
int x;
cin >> s;
if(s == "push"){
scanf("%d", &x);
q[++ tt] = x;
}else if(s == "pop"){
hh ++;
}else if(s == "empty"){
if(hh <= tt)
printf("NO\n");
else
printf("YES\n");
}else{
printf("%d\n", q[hh]);
}
// cout << endl;
}
return 0;
}
单调栈
单调栈
知识点
解题思路
- 先想一下,如果使用暴力做法,该怎么做
- 第一层循环:首先遍历数组中的每个元素
- 第二层循环:从遍历到的元素开始向前遍历,寻找第一个大于当前遍历到的元素的元素
- 使用单调栈:
- 如果$a[i] > a[j]$,那么元素$a[i]$在后续的求解过程中,一定不会被使用到,所以我们考虑将其删去
- 经过调整之后,栈序列中元素一定是单调递增的
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
int stk[N], tt;
int main(){
int n;
scanf("%d", &n);
for(int i = 0; i < n; i ++){
int x;
cin >> x;
while(tt && stk[tt] >= x)
tt --;
if(tt)
printf("%d ", stk[tt]);
else
printf("-1 ");
stk[++ tt] = x;
}
return 0;
}
单调队列
滑动窗口
解题思路
- 如果使用普通队列进行解题的话,时间复杂度需要$\Omega(nk)$
- 构建单调队列
- 求窗口中最小值时,将单调队列构建为从队头开始的到队尾的单调递增队列
- 求窗口中最大值时,将单调队列构建为从队头开始的到队尾的单调递减队列
- 单次遍历数组后,每移动一次窗口输出一次最大/最小元素
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 100;
int a[N], q[N];
int n, k;
int main(){
scanf("%d%d", &n, &k);
for(int i = 0; i < n; i ++)
scanf("%d", &a[i]);
int hh = 0, tt = -1;
for(int i = 0 ; i < n; i ++){
// 如果队头元素已经超出窗口范围
if(hh <= tt && i - k + 1 > q[hh])
hh ++;
while(hh <= tt && a[q[tt]] >= a[i])
tt --;
q[++ tt] = i;
if(i >= k - 1)
printf("%d ", a[q[hh]]);
}
cout << endl;
hh = 0, tt = -1;
for(int i = 0; i < n; i ++){
if(hh <= tt && i - k + 1 > q[hh])
hh ++;
while(hh <= tt && a[q[tt]] <= a[i])
tt --;
q[++ tt] = i;
if(i >= k - 1)
printf("%d ", a[q[hh]]);
}
cout << endl;
return 0;
}
KMP
KMP 字符串
知识点
解题思路
- 先考虑暴力算法怎么做,然后想如何去优化
- KMP习惯上从1开始
//朴素做法
for(int i = 1; i <= n; i ++){
bool flag = true;
for(int j = 1; j <= n; j ++){
if(s[i + j - 1] != s[j]){
flag = false;
break;
}
}
}

- 上方图片中,如果原字符串在与模版字符串进行匹配时,遇到了某一个字符不相等,那么我们可以进行将模版字符串进行后移的操作;后移的目的为使得原字符串和模版字符串的匹配能够继续进行。
- 这时,我们需要探究上图中绿色子串与模版字符串的开头匹配的最大值;若获取了最大值,我们就可以获取向后移动的最小距离
- 所以,我们需要对模版串进行预处理:
- 计算以某个点为后缀,从模版字符串的前缀字符串(这种字符串的第一个字符是模版字符串的字符)能够相等的最大长度是多少
- 每个点对应的长度,存储在
Next[]数组中,上面这一点也就是这个Next[]数组的含义 - 例:
- 给定
Next[i] = j,那么模版字符串p[1 ~ j] = p[i - j + 1, i](第一个字符到第j个字符构成的字符串与第i - j + 1个字符到第i个字符构成的字符串是相同的)
- 给定
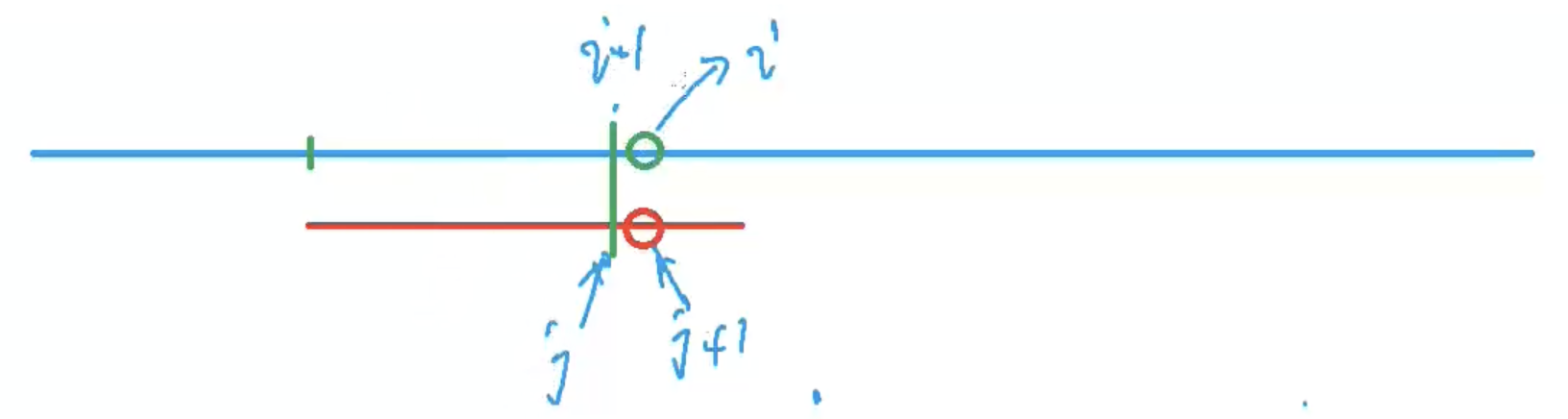
- 继续讨论
- 在上图中,设定原字符串为
S,模版字符串为P,那么可得:S[1 ~ i - 1] = P[1 ~ j]S[1 ~ i] != P[1 ~ j + 1]
- 遇到了不匹配的情况,所以我们要继续将模版字符串进行后移
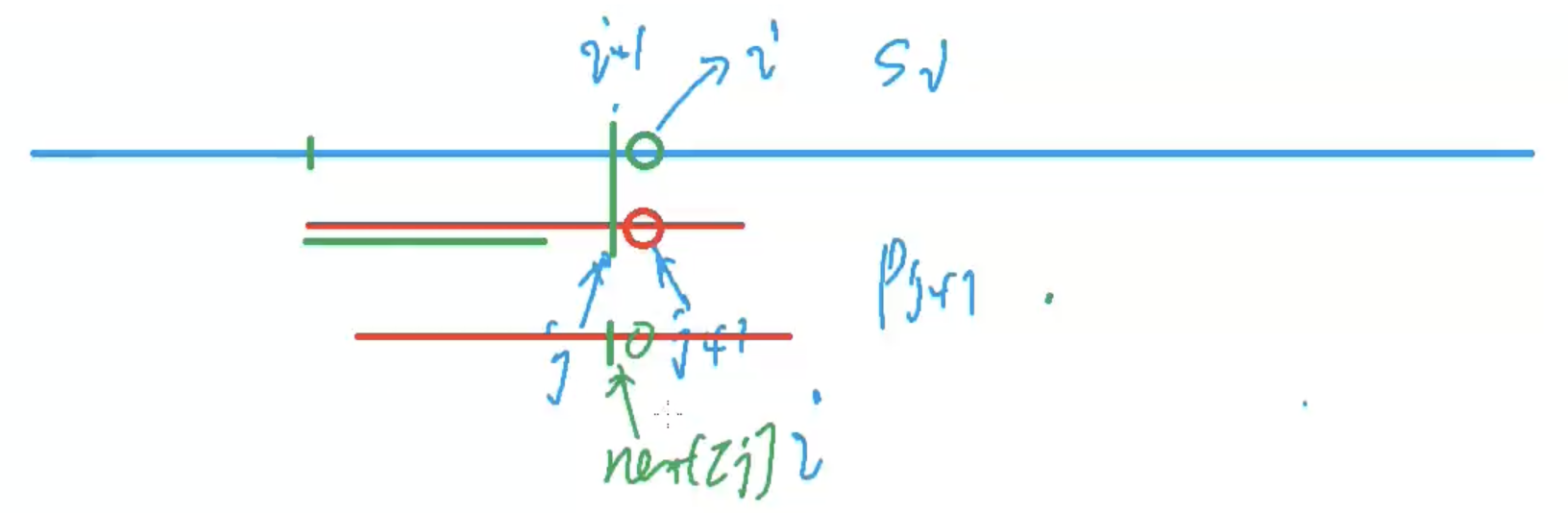
- 就将
P的第Next[j]位对准S的第i - 1位,继续检查P的第Next[j] + 1位是否与S的第i位相等- 如果相等,则继续检查
- 如果不相等,则继续后移
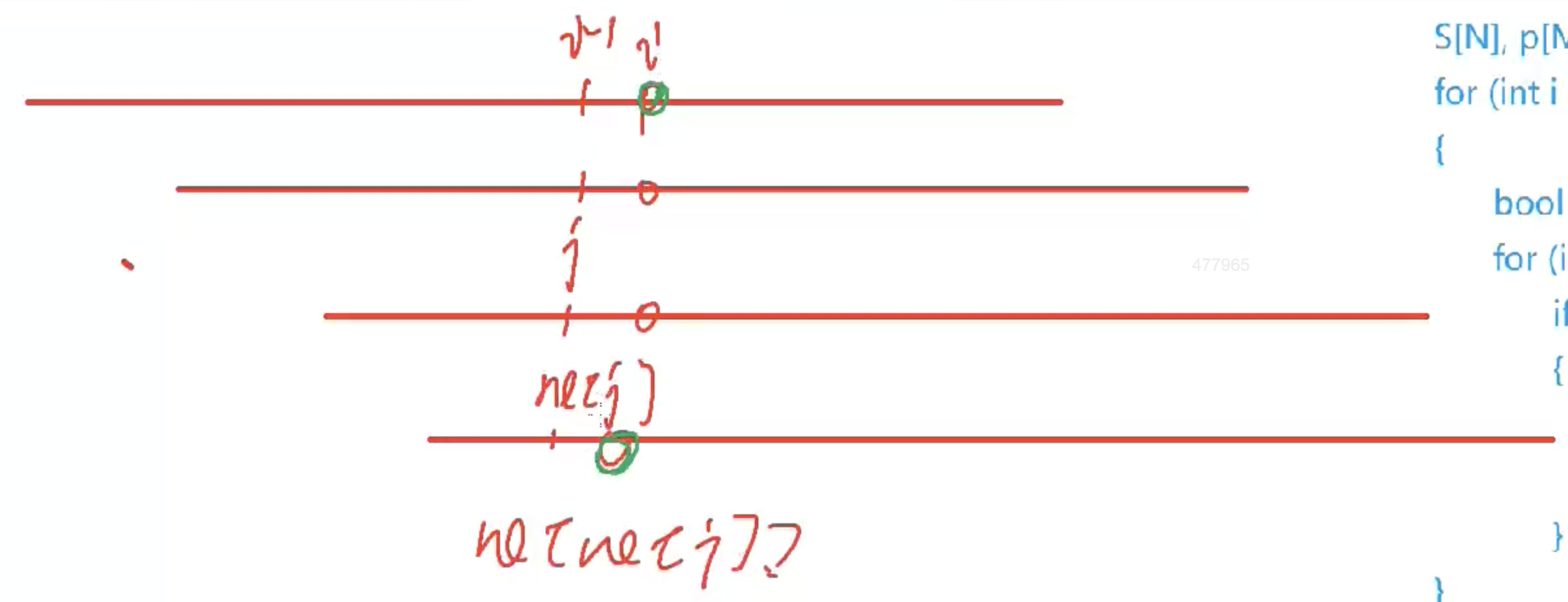
- 那么该如何求
Next[]数组呢?- 我们假定存在以字符
P[i - 1]为结尾的字符串可以与P[j]为结尾的前缀字符串进行匹配 - 接下来判断
P[i]和P[j + 1]是否匹配- 如果匹配成功,则
j ++ - 如果匹配失败,则
j = ne[j]继续进行匹配
- 如果匹配成功,则
- 我们假定存在以字符
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100, M = 1e6 + 100;
// const int N = 10010, M = 100010;
int ne[N];
int n, m;
// char s[M], p[M];
char p[N], s[M];
int main(){
cin >> n >> p + 1 >> m >> s + 1;
// 求解ne数组
for(int i = 2, j = 0; i <= n; i ++){
while(j && p[i] != p[j + 1])
j = ne[j];
if(p[i] == p[j + 1])
j ++;
ne[i] = j;
}
// 匹配过程
for(int i = 1, j = 0; i <= m; i ++){
while(j && s[i] != p[j + 1])
j = ne[j];
if(s[i] == p[j + 1])
j ++;
if(j == n){
// 匹配成功
printf("%d ", i - n);
j = ne[j];
}
}
return 0;
}
Trie
Trie字符串统计
知识点
-
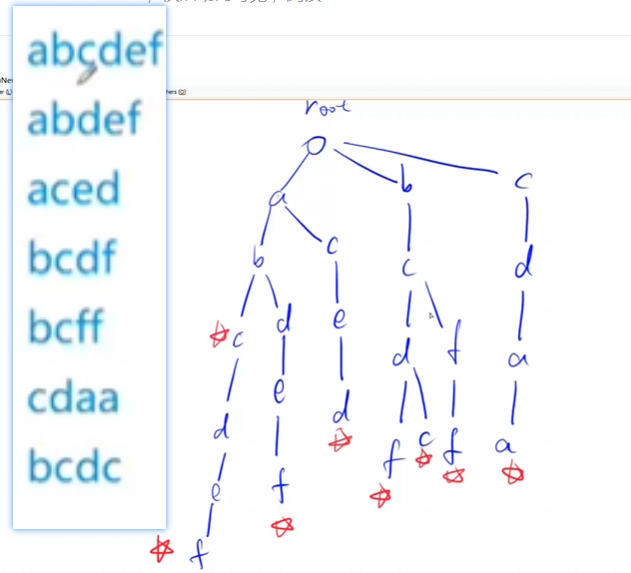
Trie:高效地存储和查找字符串的数据结构
解题思路
- 插入字符串:从头结点
root开始遍历,- 如果首字母存在则继续遍历,直至遍历到
Trie树中不存在的字符,将该字符串后面的字符作为孩子节点加入到Trie树 - 如果首字母不存在,直接将整个字符串作为孩子节点加入到头结点
root下
- 如果首字母存在则继续遍历,直至遍历到
-
对于字符串结尾的单词节点,我们使用特殊标记将其标记,已表明该节点为一个字符串的结尾
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
// son数组用来表示节点N最多有26个孩子节点,以此类推
int son[N][26], cnt[N], idx;
char str[N];
void insert(char str[]){
int p = 0;
for(int i = 0; str[i]; i ++){
// 首先将字符转化为0~25表示
int u = str[i] - 'a';
// 当前节点的孩子节点有没有当前字符
// 如果没有,则加入对应字符
if(!son[p][u])
son[p][u] = ++ idx;
// 如果有,则继续遍历
p = son[p][u];
}
cnt[p] ++;
}
int query(char str[]){
int p = 0;
for(int i = 0; str[i]; i ++){
int u = str[i] - 'a';
if(!son[p][u])
return 0;
p = son[p][u];
}
return cnt[p];
}
int main(){
int n;
cin >> n;
while(n --){
char op[2];
scanf("%s%s", op, str);
if(op[0] == 'I')
insert(str);
else
printf("%d\n", query(str));
}
return 0;
}
最大异或对


Enjoy Reading This Article?
Here are some more articles you might like to read next: