有向图的拓扑序列

知识点

只有有向无环图才有拓扑序列
拓扑序列：若一个图中所有点构成的序列$A$满足：对于图中每条边$(x,y)$，$x$在$A$中都出现在$y$之前，则称$A$是该图的一个拓扑序列

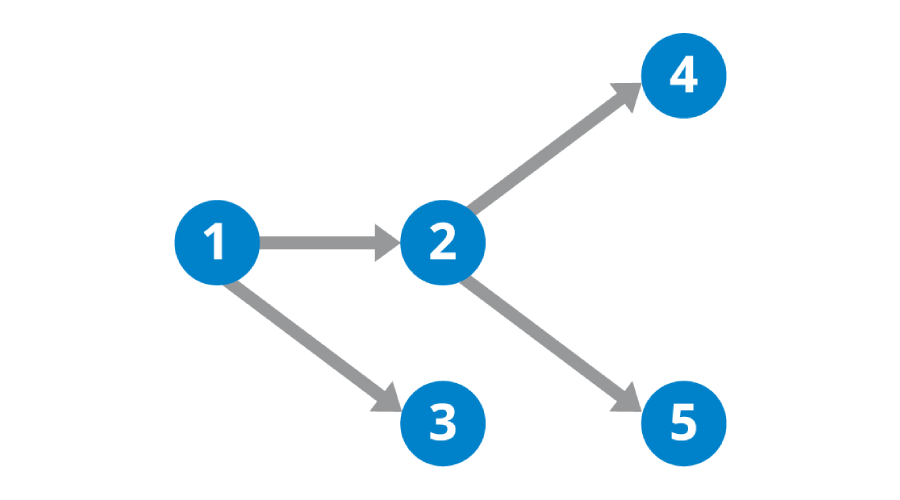
对于上面这个图，它的一个拓扑序列为$1\to 3\to 2\to 4\to 5$
度数
- 入度：一个点进来的边数
- 出度：一个点出去的边数
证明：一个有向无环图必然存在一个入度为0的点
- 使用反证法：假设在这个图中所有的点的入度都大于等于1
- 假设这个图中有$n$个店，那么我们进行$n + 1$次反向查找到上一个端点
- 根据抽屉原理，在这$n + 1$次查找中，必然有两个点是相同的，那么就说明存在着一个环
- 但是存在环与有向无环图的前提相违背，所以假设不成立
- 综上，一个有向无环图必然存在一个入度为0的点得证

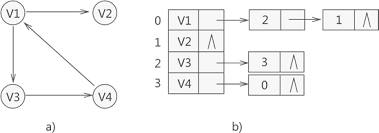
图的邻接表存储：
- 邻接表的模拟存储本质上就是使用多个单链表进行存储
- 使用h[N]数组存储头结点的信息，e[N]数组存储有向边的尾部节点，ne[idx]数组存储该点指向下一节点的指针，请注意：这里的两个结点都是以h[i]为头结点的有向边指向的终点结点，这就是一个头插法
- 举一个具体的例子，假设我们要加入一条从a指向b的有向边，我们首先初始化端点b，这个端点指向下一节点的指针等于h[a],更新h[a]指向下一节点的指针为idx，并将idx ++

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;

int n, m;
int h[N], e[N], ne[N], idx;

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int main(){
    cin >> n >> m;

    for(int i = 0; i < m; i ++){
        int a, b;
        cin >> a >> b;
        add(a, b);

    }
}

解题思路

寻找入度为0的点都可以作为拓扑序列最前面的元素，把所有入度为0的点入队
进行BFS
- 当队列不为空时，将队列头元素出队，设为t
- 依次枚举t的所有出边$\text{t} \to \text{j}$
- 删掉$\text{t} \to \text{j}$，更新j的入度d[j] --
- if(d[j] == 0)，说明j前面的所有元素都已经遍历完毕，j可以入队

实现代码

y总照抄版

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;

int q[N], d[N];


void add (int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool toposort(){
    int hh = 0, tt = -1;

    for(int i = 1; i <= n; i ++){
        if(!d[i])
            q[++ tt] = i;
    }

    while(hh <= tt){
        int t = q[hh ++];

        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(-- d[j] == 0){
                q[++ tt] = j;
            }
        }
    }

    return tt == n - 1;
}


int main(){
    cin >> n >> m;
    memset(h, -1, sizeof h);

    for(int i = 0; i < m; i ++){
        int a, b;
        cin >> a >> b;
        add(a, b);

        d[b] ++;
    }

    if(!toposort())
        cout << "-1" << endl;
    else{
        for(int i = 0 ; i < n; i ++)
            cout << q[i] << " ";
    }

    return 0;
}

20250213理解了之后重写了一版

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 100;

int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1;
int n, m;
int d[N];

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void toposort(){
    for(int i = 1; i <= n; i ++){
        if(!d[i])
            q[++ tt] = i;
    }

    while(tt >= hh){
        int a = q[hh ++];
        for(int i = h[a]; i != -1; i = ne[i]){
            int b = e[i];
            if(-- d[b] == 0)
                q[++ tt] = b;

        }
    }

    if(tt == n - 1){
        for(int i = 0; i <= tt; i ++){
            cout << q[i] << " ";
        }
    }else{
        cout << -1;
    }

    cout << endl;
}


int main(){
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m;

    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++){
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b] ++;
    }

    toposort();
    return 0;


}

拓扑排序

有向图的拓扑序列

知识点

解题思路

实现代码

y总照抄版

20250213理解了之后重写了一版

Enjoy Reading This Article?