双指针问题

Created in February 03, 2025

2025   ·   code   algorithm   acwing   ·   learning-notebook

最长连续不重复子序列

解题思路

双指针算法的样子

for(int i = 0, j = 0; i < n; i ++){
	while(j < i && check(i, j)) j ++;
	// 每道题的具体逻辑
}
  • 最核心的性质：可以优化

核心思想

for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++)
		//代码实现的逻辑
}
  • 可以将$\Omega(n^2)$的朴素算法优化到$\Omega(n)$

最长连续不重复子序列

Snipaste_2025-01-31_12-38-16.png

  • 给定绿色右侧指针为当前的j（对于j的定义为：j往左能到的符合条件的、最远的地方），绿色左侧指针为假设我们还有一个j能更加左，但是这个与j的定义相矛盾，所以我们说j到i之间的距离就是最长连续不重复子序列的长度
  • 基本代码模版为：
// 朴素做法，复杂度为O(n)
for(int i = 0; i < n; i ++){
	for(int j = 0; j < n; j ++){
		if(check(i, j)){
			res = max(res, i - j + 1);
		}
	}
}
// 双指针算法
// 发现一些单调性质，并利用
for(int i = 0; i < n; i ++){
	while(j <= i && check(i, j)){
		j ++;
	}

	res = max(res, i - j + 1);

}

代码实现

双指针算法最基本的应用

  • 提取用空格分隔开的单词
#include <bits/stdc++.h>

using namespace std;

int main(){
	char str[100];
	gets(str);
//	这里一定要使用gets()，使用cin会导致第一个空格之后的字符没有被提取到
//	cout << str << endl;
//	cin 使用 >> 运算符的时候，默认会跳过空白字符，直到遇到下一个空白字符停止读取
// 	所以cin只能读取到第一个单词

	int n = strlen(str);

	for(int i = 0; i < n; i ++){
		int j = i;
		while(j < n && str[j] != ' '){

			j ++;

		}

		for(int k = i; k < j; k ++){
			cout << str[k];
//			注意 k ++ 这个语句是在一个循环块执行结束后执行
		}
		cout << endl;

		i = j;
	}


	return 0;

}

![[Pasted image 20250131121856.png]]

最长连续不重复子序列

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 100;
int n;
int a[N], s[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }

    int res = 0;
    for(int i = 0, j = 0; i < n; i ++){
        s[a[i]] ++;
        while(s[a[i]] > 1){
            s[a[j]] --;
            j ++;
        }

        res = max(res,i - j + 1);
    }


    cout << res << endl;

    return 0;
}

数组元素的目标和

实现思想

  • 暴力做法（容易超时）
  • 找单调性：
    • 主要思路是for(int i = 0; i < n; i ++)，找到一个j，使得$A_i+B_j\geq x$，同时j的下标是最小的
    • 当有满足条件的下标i, j出现的时候，直接输出答案并break

实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 100;
int n, m, x;
int a[N], b[N];

int main(){
    cin >> n >> m >> x;
    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }
    for(int i = 0; i < m; i ++){
        cin >> b[i];
    }

    for(int i = 0, j = m - 1; i < n; i ++){

        while(j >= 0 && a[i] + b[j] > x){
            j --;
        }
        if(a[i] + b[j] == x){
            cout << i << " " << j << endl;
            break;
        }
    }
}

判断子序列

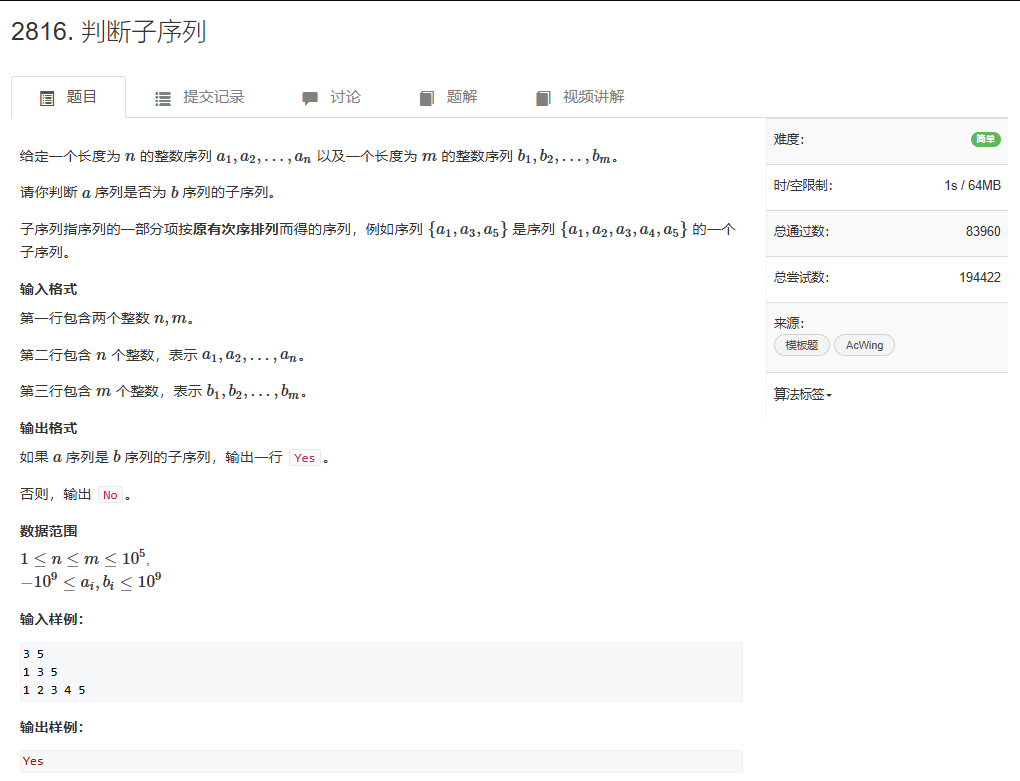
解题思路

  • 对数组B中的每一个元素进行遍历，如果出现了一个数组A中的元素相同的元素（第一个），就将其与数组A中的映射关系记录下来
  • 如果遍历完数组B，数组A中的每个元素都找到了，那么我们可以说数组B中存在一个数组A的子序列的匹配
  • 下面我们需要证明，如果数组B存在着数组A的子序列，那么上述算法一定可以找出一种匹配
    • 假定数组B中存在着一组匹配，我们遍历数组A的每个元素，在数组B中寻找与之匹配的元素
    • 如果找到了一个与数组A中元素相同，但是这个元素位于匹配中对应元素之前，如上图虚线所示（实线为假定的匹配）。
    • 我们可以将实线的匹配，替换为虚线的匹配。这样做我们发现，这其实是不会影响后续的匹配的，即说明，使用双指针算法可以找到存在的合法匹配。
  • 在这种类似于“贪心”的算法中，证明充分必要性是很重要的，在本题中：
    • 充分性：如果双指针算法找到了一个匹配，那么这确实是一个合法的子序列匹配
    • 必要性：如果存在一个合法的子序列匹配，那么双指针算法一定能够找到一个合法的匹配
    • 证明必要性的原因：通过证明必要性，即使存在其他的匹配，我们也可以证明即使是“贪心”地选择了第一个（相对地）匹配的元素，那么形成的匹配也是合法的。

实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 100;
int a[N], b[N];
int n, m;

int main(){
    cin >> n >> m;

    for(int i = 0; i < n; i ++){
        cin >> a[i];
    }

    for(int i = 0; i < m; i ++){
        cin >> b[i];
    }

    int i = 0, j = 0;
    while(i < n && j < m){
        if(a[i] == b[j]){
            i ++;
        }
        j ++;
    }
    if(i == n){
        cout << "Yes" << endl;
    }else{
        cout << "No" << endl;
    }

    return 0;

}

力扣习题

移动零

实现思路&需要注意的点

  • 初始化两个指针l和r
  • 当r指针指向的数字为0时，指针r向后移动
  • 当r指针指向的数字不为0时，指针l, r向后移动，并将l, r分别指向的两个数字进行交换
  • 进行以上操作之后的效果为：
    • 指针l左侧全为非零数字
    • 指针r和l之间都是零
  • 当指针r移动到末尾时，操作完毕，此时的数字已经满足要求

实现代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size();
        int left = 0, right = 0;
        while(right < n){
            // left 和 right指针之间都是0
            if(nums[right]){
                swap(nums[left], nums[right]);
                left ++;
            }
            right ++;

        }
    }
};

盛水最多的容器

实现思路&需要注意的点

  • 我们可以发现，在高度中，影响装的水的体积的因素，是两个高度中较矮的那个，即“木桶效应”
进行数学证明
  1. 给定heights数组存储所有木板的长度
  2. 假设初始化两个指针l和r，其中l位于数组下标0处，r位于数组最末端（下标为数组长度减1）
  3. 假设heights[l]<heights[r]，那么我们可以得到，当前装载水的体积为heights[l] * (r - l)。
  4. 如果我们此时移动r指针，那么水的体积会怎么变化呢？从下面的推断，可以发现移动r指针（高度较高的那个）是不会让水的体积变大的
    • 如果heights[r_new] <= heights[r]，那么新的水体积min(heights[r_new], heights[l]) <= heights[l] * (r - l)
    • 如果heights[r_new] > heights[r]，那么新的水的体积min(heights[r_new], heights[l]) > heights[l] * (r - l)
  5. 我们应该移动l指针（高度较低的指针），才可能使得水体积变大
    • 如果heights[l_new] <= heights[l]，那么新的水体积一定小于等于原来的
    • 如果heights[l_new] > heights[l]，那么新的水体积是大于原来水体积的
  6. 综上所述，应该移动指向高度较低的指针，并向对侧移动（l ++和r --），才能找到能盛水最多的容器壁

实现代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        // int ans = 0;
        int n = height.size();
        int l = 0, r = n - 1;
        int ans = (n - 1) * min(height[l], height[r]);
        while(l < r){
            int h = min(height[r], height[l]);
            ans = max(ans, (r - l) * h);
            if(height[l] > height[r])
                h = height[r --];
            else
                h = height[l ++];

        }
        return ans;
    }
};

三数之和

基础知识

  • vector的find函数的使用方法：
    • find(vec.begin(),vector.end(), val)
    • 返回的是一个迭代器
    • 如果找到了，返回的是对应元素的迭代器
    • 如果没找到返回的是

解题思路

  • 这道题其实也可以仿照双指针经典题目“两数之和”进行求解
  • 其中不同的地方在于，“两数之和”问题在获得解之后，立即break跳出循环，而我们这道题还需要继续寻找
  • 解决方法：
    • 其实这道题是“三指针”问题
    • 我们首先确定i，指针i遍历数组中的每一个数字
    • 接下来确定l和r指针，从这里开始我们将问题转化为“两数之和”
      • 首先初始化l和r的位置，其中l位于i+1的位置，r位于数组的最后一位，两个指针向数组的中央移动。为什么呢？这是因为我们解决双指针问题，需要利用单调性，确保一个指针移动的时候，另一个指针的移动是单调的，这样我们才能确保解题的唯一性！
      • 另外一个是循环终止条件，我认为我第一次的解题TLE，主要是因为这里的循环终止条件（break条件）设置的不好
      • 我们设置的终止条件为l == r，此时如果l继续向右移动，获得的元素只会更大，无论如何也不可能满足nums[l] + nums[r] == target

实现代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        for(int i = 0; i < n; i ++){
            if(i > 0 && nums[i] == nums[i - 1]){
                continue;
            }

            int r = n - 1;
            // l从最左边，r从最右边开始，利用了数组排序后的单调性
            int target = -nums[i];

            for(int l = i + 1; l < n; l ++){
                if(l > i + 1 && nums[l] == nums[l - 1]){
                    continue;
                }
                while(l < r && nums[l] + nums[r] > target){
                    r --;
                }
                // 如果l == r，那么之后一定不会出现nums[l] + nums[r] = target(l < r)
                // 如果l继续移动的话，和会越来越大，不会找到目标值的
                // 所以break就ok了
                if(l == r){
                    break;
                }

                if(nums[l] + nums[r] == target){
                    ans.push_back({nums[i], nums[l], nums[r]});
                }
            }
        }
        return ans;
    }
};

这个是我研究1h的代码，最后TLE了，🥲

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>> ans;
        if(nums.size() == 3){
            if(nums[0] + nums[1] + nums[2] == 0){
                ans.push_back(nums);
            }
            return ans;
        }


        for(int i = 0; i < nums.size() - 2; i ++){
            if(i != 0 && nums[i] == nums[i - 1]){
                continue;
            }
            int target = -nums[i];
            for(int l = i + 1, r = nums.size() - 1; l < nums.size(); l ++){
                if(nums[i] > 0 && nums[r] > 0){
                    break;
                }

                vector<int> temp;
                while(r > l && nums[l] + nums[r] > target && nums[l] + nums[r] >= 0){
                    r --;
                }
                if(nums[l] + nums[r] == target && l != r){
                    printf("%d %d %d\n", i, l, r);
                    temp.push_back(nums[i]);
                    temp.push_back(nums[l]);
                    temp.push_back(nums[r]);

                }
                if(temp.size()){
                    // sort(temp.begin(),temp.end());
                    // auto it = find(ans.begin(),ans.end(),temp);
                    // if(it == ans.end()){
                    //     ans.push_back(temp);
                    // }
                    ans.push_back(temp);
                }
                if(nums[i] == 0 && nums[r] == 0)
                    break;

            }

        }
        return ans;
    }
};

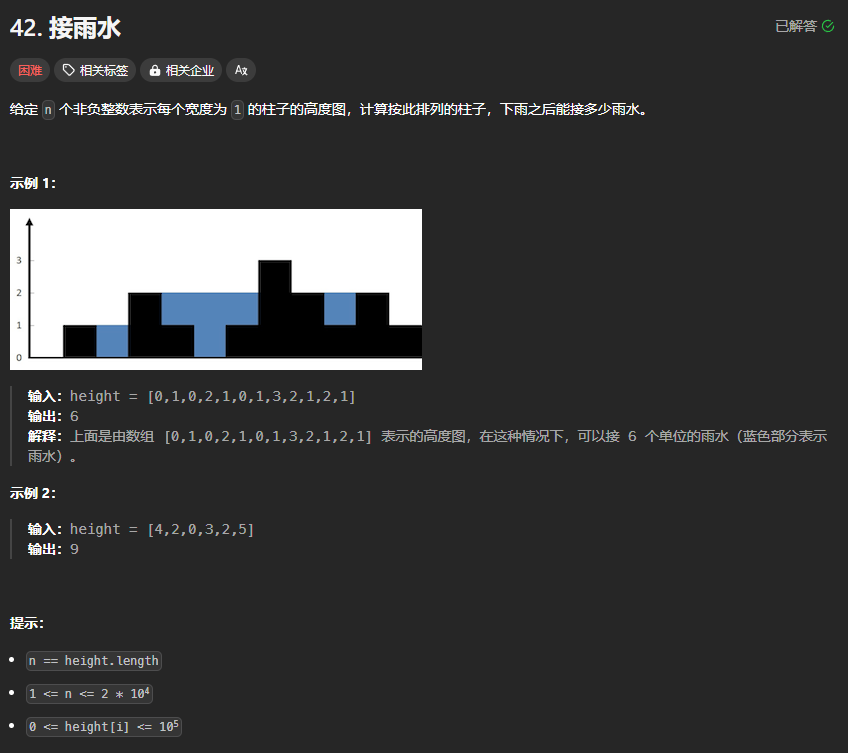
接雨水



Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • Google Gemini updates: Flash 1.5, Gemma 2 and Project Astra
  • Displaying External Posts on Your al-folio Blog
  • 强化学习导论
  • 企业项目实训
  • 面试总结